
分析 根据运动的规则找出点P、Q表示的数,分P、O、Q三点位置不同考虑,根据三等分点的性质列出关于时间t的一元一次方程,解方程即可得出结论.
解答 解:设运动的时间为t(t>0),则点P表示3t-16,点Q表示t+14,
①当点O在线段AB上时,如图1所示.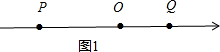
此时3t-16<0,即t<$\frac{16}{3}$.
∵点O是线段PQ的三等分点,
∴PO=2OQ或2PO=OQ,
即16-3t=2(t+14)或2(16-3t)=t+14,
解得:t=-$\frac{12}{5}$(舍去),或t=$\frac{18}{7}$;
②当点P在线段OQ上时,如图2所示.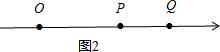
此时0<3t-16<t+14,即$\frac{16}{3}$<t<15.
∵点P是线段OQ的三等分点,
∴2OP=PQ或OP=2PQ,
即2(3t-16)=t+14-(3t-16)或3t-16=2[t+14-(3t-16)],
解得:t=$\frac{31}{4}$,或t=$\frac{76}{7}$;
③当点Q在线段OP上时,如图3所示.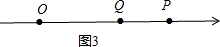
此时t+14<3t-16,即t>15.
∵点Q是线段OP的三等分点,
∴OQ=2QP或2OQ=QP,
即t+14=2[3t-16-(t+14)]或2(t+14)=3t-16-(t+14),
解得:t=$\frac{74}{3}$,或无解.
综上可知:点P,Q,O三点在运动过程中,其中两点为端点构成的线段被第三个点三等分,则运动时间为$\frac{18}{7}$、$\frac{31}{4}$、$\frac{76}{7}$或$\frac{74}{3}$秒.
故答案为:$\frac{18}{7}$、$\frac{31}{4}$、$\frac{76}{7}$或$\frac{74}{3}$.
点评 本题考查了一元一次方程的应用以及数轴,解题的关键是按P、O、Q三点位置不同分类讨论.本题属于中档题,难度不大,解决该题型题目时,根据运动的过程分情况考虑,再根据三等分点的性质列出方程是关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:选择题
 中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1,S2,S3,若S1+S2+S3=18,则正方形EFGH的面积为( )
中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1,S2,S3,若S1+S2+S3=18,则正方形EFGH的面积为( )| A. | 9 | B. | 6 | C. | 5 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
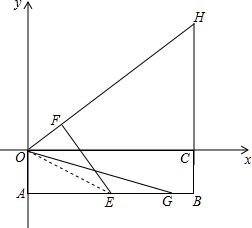 如图,矩形OABC中,OA在y轴的负半轴上,OC在x轴的正半轴上,OA=1,OC=4,E是AB的中点,将矩形沿OE折叠,点A与点F重合,延长OF、BC交于点H,G是射线AB上一点,将△OAG绕点O旋转,使得点A落在OE上,记旋转后的三角形为△OA′G′,A′G′与OH交于点M,若∠MHG′=∠MHB,则AG的长为$\frac{2+20\sqrt{5}}{11}$.
如图,矩形OABC中,OA在y轴的负半轴上,OC在x轴的正半轴上,OA=1,OC=4,E是AB的中点,将矩形沿OE折叠,点A与点F重合,延长OF、BC交于点H,G是射线AB上一点,将△OAG绕点O旋转,使得点A落在OE上,记旋转后的三角形为△OA′G′,A′G′与OH交于点M,若∠MHG′=∠MHB,则AG的长为$\frac{2+20\sqrt{5}}{11}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
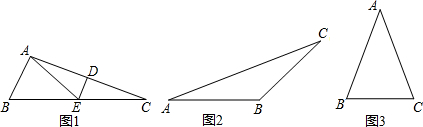
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
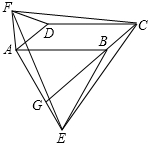 如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G落在点A、E之间,连接EF、CF.则以下四个结论:
如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G落在点A、E之间,连接EF、CF.则以下四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
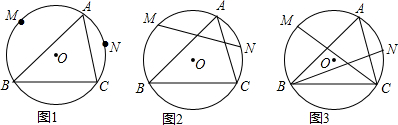
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
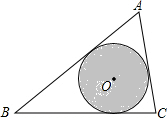 如图,△ABC中,AB=8,AC=5,∠A=60°,圆O是三角形的内切圆,如果在这个三角形内随意抛一粒豆子,则豆子落在圆O内的概率为$\frac{\sqrt{3}π}{10}$.
如图,△ABC中,AB=8,AC=5,∠A=60°,圆O是三角形的内切圆,如果在这个三角形内随意抛一粒豆子,则豆子落在圆O内的概率为$\frac{\sqrt{3}π}{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com