
【题目】如图,长方形ABCD中,AB=4cm,BC=3cm,点E是CD的中点,动点P从A点出发,以每秒1cm的速度沿A→B→C→E 运动,最终到达点E.若点P运动的时间为x秒,那么当x= _________时,△APE的面积等于![]() .
.

 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】2018年,新疆某次足球联赛规定每队胜一场得3分,平一场得1分,负一场得0分,某队前14场保持不败,共得32分,设该队平了x场,根据题意列方程得:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时,画出图形,写出“已知”,“求证”(如图),她们对各自所作的辅助线描述如下:

文文:“过点A作BC的中垂线AD,垂足为D”;
彬彬:“作△ABC的角平分线AD”.
数学老师看了两位同学的辅助线作法后,说:“彬彬的作法是正确的,而文文的作法需要订正.”
(1)请你简要说明文文的辅助线作法错在哪里;
(2)根据彬彬的辅助线作法,完成证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.﹣1的平方根是﹣1
B.4的平方根是2
C.如果一个数有平方根,那么这个数的平方根一定有两个
D.任何一个非负数的立方根都是非负数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O1、⊙O2相交于P、Q两点,其中⊙O1的半径r1=2,⊙O2的半径r2= ![]() .过点Q作CD⊥PQ,分别交⊙O1和⊙O2于点C、D,连接CP、DP,过点Q任作一直线AB交⊙O1和⊙O2于点A、B,连接AP、BP、AC、DB,且AC与DB的延长线交于点E.
.过点Q作CD⊥PQ,分别交⊙O1和⊙O2于点C、D,连接CP、DP,过点Q任作一直线AB交⊙O1和⊙O2于点A、B,连接AP、BP、AC、DB,且AC与DB的延长线交于点E. 
(1)求证: ![]() ;
;
(2)若PQ=2,试求∠E度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(﹣1,0),B(4,0),点C在y轴的正半轴上,且∠ACB=90°,抛物线y=ax2+bx+c经过A、B、C三点,其顶点为M.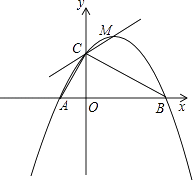
(1)求抛物线y=ax2+bx+c的解析式;
(2)试判断直线CM与以AB为直径的圆的位置关系,并加以证明;
(3)在抛物线上是否存在点N,使得S△BCN=4?如果存在,那么这样的点有几个?如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com