已知抛物线y=-x2+2(k-1)x+k+2与x轴交于A、B两点,且点A在x轴的负半轴上,点B在x轴的正半轴上.
(1)求实数k的取值范围;
(2)设OA、OB的长分别为a、b,且a:b=1:5,求抛物线的解析式;
(3)在(2)的条件下,以AB为直径的⊙D与y轴的正半轴交于P点,过P点作⊙D的切线交x轴于E点,求点E的坐标.
【答案】
分析:(1)由于A、B分别在x轴的正负半轴上,由此可得出A、B两点横坐标的积应该是负数,即-(k+2)<0,由此可得出k的取值范围;
(2)可根据OA、OB的比例关系设出A、B两点的横坐标(要注意A点在负半轴上),然后根据根与系数的关系即可得出一个关于k的方程组,进而可求出k的值,也就求出了抛物线的解析式;
(3)求E点的坐标就是求OE的长,已知了A、B的坐标可求出D的坐标,以及圆D的半径长,如果连接DP,在直角三角形OPE中,可用射影定理得出DP
2=OD•DE即r
2=OD•DE,由此可求出DE的长,已知D的坐标,可据此求出E的坐标.
解答:
解:(1)设点A(x
1,0),B(x
2,0)且满足x
1<0<x
2由题意可知x
1x
2=-(k+2)<0,即k>-2.
(2)∵a:b=1:5,设OA=a,即-x
1=a.
则OB=5a,即x
2=5a,a>0
∴

,即
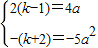
∴k=2a+1,
即5a
2-2a-3=0,解得a
1=1,
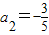
(舍去)
∴k=3
∴抛物线的解析式为y=-x
2+4x+5.
(3)由(2)可知,当-x
2+4x+5=0时,可得x
1=-1,x
2=5.
即A(-1,0),B(5,0),
∴AB=6,则点D的坐标为(2,0)
当PE是⊙D的切线时,PE⊥PD
由Rt△DPO∽Rt△DEP可得PD
2=OD•DE
即3
2=2×DE
∴DE=

,OE=DE-OD=

-2=

,
故点E的坐标为(-

,0).
点评:本题着重考查了待定系数法求二次函数解析式、二次函数与一元二次方程的关系、一元二次方程根与系数的关系、切线的性质等重要知识点,综合性较强.

 解:(1)设点A(x1,0),B(x2,0)且满足x1<0<x2
解:(1)设点A(x1,0),B(x2,0)且满足x1<0<x2 ,即
,即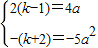
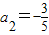 (舍去)
(舍去) ,OE=DE-OD=
,OE=DE-OD= -2=
-2= ,
, ,0).
,0).

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.