练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，货轮O在航行过程中，发现灯塔A在它南偏东60°的方向上，同时，在它北偏东30°、西北（即北偏西45°）方向上又分别发现了客轮B和海岛C．

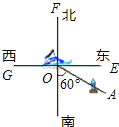
    （1）仿照表示灯塔方位的方法，分别画出表示客轮B和海岛C方向的射线OB，OC（不写作法）；

    （2）若图中有一艘渔船D，且∠AOD的补角是它的余角的3倍，画出表示渔船D方向的射线OD，则渔船D在货轮O的 （写出方位角）

    【答案】（1）见解析；（2）D在O南偏东15°或北偏东75°．

    【解析】

    试题分析：（1）根据方向角的度数，可得答案；

    （2）根据余角与补角的关系，可得∠AOD的度数，根据角的和差，可得方向角．

    解：（1）如图1：

    ，

    （2）如图2：

    ，

    由∠AOD的补角是它的余角的3倍，得

    180°﹣∠AOD=3（180°﹣∠AOD）．

    解得∠AOD=45°．

    故D在O南偏东15°或北偏东75°．

    故答案为：D在O南偏东15°或北偏东75°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】作图与计算

    （1）已知：．

    求作：在图2中，以OA为一边，在∠AOB的内部作．∠AOC＝（要求：直尺和圆规作图，不写作法，保留图痕迹．）

    （2）过点O分别引射线OA、OB、OC，且∠AOB=65°，∠BOC=30°，求∠AOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABE≌△ACD．

    （1）如果BE=6，DE=2，求BC的长；

    （2）如果∠BAC=75°，∠BAD=30°，求∠DAE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AC⊥BC，DC⊥EC，AC=BC，DC=EC．

    （1）求证：AE=BD；

    （2）判断AE与BD的位置关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

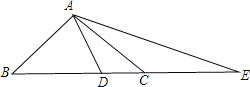
    【题目】(1)如图，在在△ABC中，已知∠BAC=900，AB=AC,点D在BC上，且BD=BA，点E在BC的延长线上，CE=CA，求∠DAE的度数；

    (2)如果把（1）中的“AB=AC”条件去掉，其余条件不变，那么∠DAE的度数改变吗？为什么？

    (3)如果把（1）中的“∠BAC=900”改成“∠BAC>900”其余条件不变，试探究∠DAE与∠BAC的数量关系式，试证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

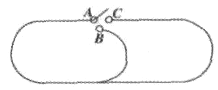
    【题目】如图是一个玩具火车轨道，点A有个变轨开关，可以连接点B或点C.小圈轨道的周长是2米，大圈轨道的周长是4米.开始时，点A连接点C，火车从点A出发，按照顺时针方向在轨道上移动，同时变轨开关每隔一分钟变换一次轨道连接.若火车的速度是每分钟10米，则火车第10次回到A点时用了 分钟.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解学生最喜爱的球类运动，某初中在全校2000名学生中抽取部分学生进行调查，要求学生只能从“A（篮球）、B（羽毛球）、C（足球）、D（乒乓球）”中选择一种．

    （1）小明直接在八年级学生中随机调查了一些同学．他的抽样是否合理？请说明理由．

    （2）小王从各年级随机抽取了部分同学进行调查，整理数据，绘制出下列两幅不完整的统计图．请根据图中所提供的信息，回答下列问题：

    ①请将条形统计图补充完整；

    ②估计该初中最喜爱乒乓球的学生人数约为　 　人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

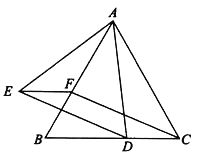
    【题目】如图，在等边△ABC中，D，F分别为CB，BA上的点，且CD＝BF，以AD为边作等边三角形ADE。

    求证：（1）△ACD≌△CBF；

    （2）四边形CDEF为平行四边形.

    查看答案和解析>>

    同步练习册答案