
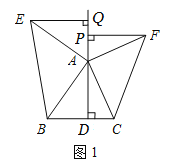
【题目】如图①,ΔABC中,AD⊥BC于点D,以A为直角顶点,分别以AB、AC为直角边,向ΔABC外作等腰RtΔABE和等腰RtΔACF,过点E、F作射线DA的垂线,垂足分别为Q、P.
(1)试探究线段EQ和FP之间的数量关系,并说明理由.
(2)如图②,若连接EF交DA的延长线于点H,由(1)中的结论你能判断EH与FH的大小关系吗?并说明理由.
(3)图②中的ΔABC与ΔAEF的面积相等吗?(直接给出结论,不需要说理)


【答案】(1)EQ=FP,理由见解析;(2)HE=HF,理由见解析;(3)相等,理由见解析.
【解析】
(1)根据AAS得出△EAQ≌△ABD,可得EQ=AD,同理AD=FP,由此可得结论;
(2)过点E作EQ⊥DA,过点F作FP⊥DA,垂足分别为Q、P.根据AAS证明△EQH≌△FPH即可;
(3)由(1)、(2)中的全等三角形可以推得△ABC与△AEF的面积相等.
解:(1)EQ=FP,理由如下:
如图1,∵Rt△ABE是等腰三角形,∴EA=BA.
∵∠QEA+∠QAE=90°,∠QAE+∠BAD=90°,
∴∠QEA=∠BAD.
在△EAQ与△ABD中,
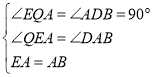 ,
,
∴△EAQ≌△ABD(AAS),
∴EQ=AD.
同理AD=FP.
∴EQ=FP.
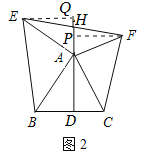
(2)HE=HF,理由如下:
如图2,过点E作EQ⊥DA,过点F作FP⊥DA,垂足分别为Q、P.
由(1)知EQ=FP.
在△EQH与△FPH中,
∵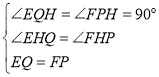 ,
,
∴△EQH≌△FPH(AAS).
∴HE=HF;
(3)相等.理由如下:
由(1)知,△ABD≌△EAQ,△FPA≌△ADC,则S△ABD=S△EAQ,S△FPA=S△ADC.
由(2)知,△EQH≌△FPH,则S△EQH=S△FPH,
所以S△ABC=S△ABD+S△ADC=S△EAQ﹣S△EQH+S△FPA﹣S△FPH=S△EAH+S△FHA=S△AEF,即S△ABC=S△AEF.
故图②中的△ABC与△AEF的面积相等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】证明命题“对角线相等的平行四边形是矩形”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小张同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,ABCD是平行四边形,AC与BD是对角线,且 .
求证: .
请你补全已知和求证,并写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,BC=2![]() .点P从点A出发沿沿射线AB以1
.点P从点A出发沿沿射线AB以1![]() 的速度运动,过点P作PE∥BC交射线AC于点E,同时点Q从点C出发沿BC的延长线以1
的速度运动,过点P作PE∥BC交射线AC于点E,同时点Q从点C出发沿BC的延长线以1![]() 的速度运动,连结BE、EQ.设点P的运动时间为t(
的速度运动,连结BE、EQ.设点P的运动时间为t(![]() ).
).

(1)求证:△APE是等边三角形;
(2)直接写出CE的长(用含![]() 的代数式表示);
的代数式表示);
(3)当点P在边AB上,且不与点A、B重合时,求证:△BPE≌△ECQ.
(4)在不添加字母和连结其它线段的条件下,当图中等腰三角形的个数大于3时,直接写出t的值和对应的等腰三角形的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边三角形AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,连接DA并延长,交y轴于点E.
①△OBC与△ABD全等吗?判断并证明你的结论;
②当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,∠ABC为锐角,AB<BC,点E是AD上的一点,延长CE到F,连接BF交AD于点G, 使∠FBC=∠DCE.
⑴ 求证:∠D=∠F;
⑵ 在直线AD找一点P,使以点B、P、C为顶点的三角形与以点C、D、P为顶点的三角形相似.(在原图中标出准确P点的位置,必要时用直尺和圆规作出P点,保留作图的痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B是⊙O上的两点,∠AOB=120°,C是![]() 的中点.
的中点.
(1)如图1,求∠A的度数;
(2)如图2,延长OA至点D,使OA=AD,连接DC,延长OB交DC的延长线于点E.若⊙O的半径为1,求DE的长.

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.
(1)求证:四边形ABEF是平行四边形;
(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com