
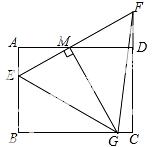
如图,矩形ABCD中,AB=3,AD=4,E为AB上一点,AE=1,M为射线AD上一动点,AM=a(a为大于0的常数),直线EM与直线CD交于点F,过点M作MG⊥EM,交直线BC于G.
(1)若M为边AD中点,求证:△EFG是等腰三角形;
(2)若点G与点C重合,求线 段MG的长;
段MG的长;
(3)请用含a的代数式表示△EFG的面积S,并指出S的最小整数值.
 长度,然后用含a的代数式表示△EFG的面积S,指出S的最小整数值.
长度,然后用含a的代数式表示△EFG的面积S,指出S的最小整数值.

又∵∠MCD+∠MFD=90°,∠AME+∠AEM=9 0°,∴∠AME=∠MCD.
0°,∴∠AME=∠MCD.
∵∠MAE=∠CDM=90°,∴△MAE∽△CDM. ∴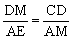 ,即
,即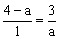 ,解得a=1或3.
,解得a=1或3.
代入CM=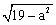 得CM=
得CM=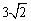 或
或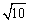 .
.
∵点G与点C重合,∴MG=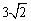 或
或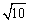 .
.
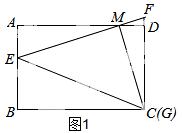
(3)①当点M在AD上时,如答图2,过点M作MN⊥BC交BC于点N,
∵AB=3,AD=4,AE=1,AM=a。∴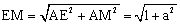 ,MD=AD-AM=4-a.
,MD=AD-AM=4-a.
∵∠A=∠MDF=90°,∠AME=∠DMF, ∴△MAE∽△MDF. ∴
∴△MAE∽△MDF. ∴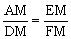 ,即
,即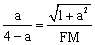 .
.
∴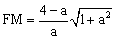 .∴
.∴ .
.
∵AD∥BC,∴∠MGN=∠DMG.
∵∠AME+∠AEM=90°,∠AME+∠DMG=90°,∴∠AME=∠DMG. ∴∠MGN=∠AME.

②当点M在AD的延长线上时,如图3,过点M作MN⊥BC,交BC延长线于点N,
∵AB=3,AD=4,AE=1,AM=a,∴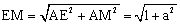 ,MD=a-4.
,MD=a-4.
∵DC∥AB,∴△MAE∽△MDF.∴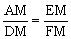 ,即
,即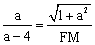 .∴
.∴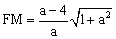 .
.
∴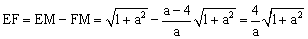 .
.
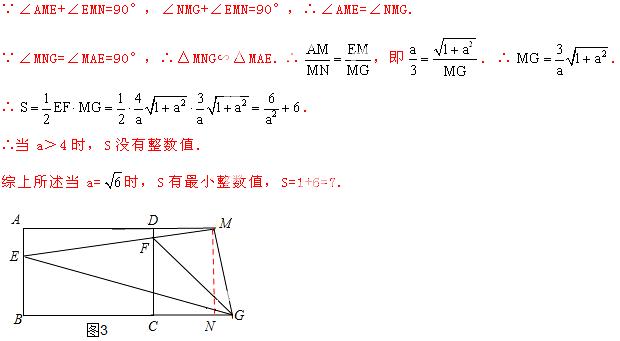
考点:1.单动点问题;2.矩形的性质;3.全等三角形的判定和性质;4. 等腰三角形的判定和;5.勾股定理;6.相似三角形的判定和性质;7.分类思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )
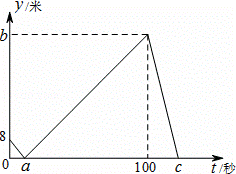
A. ①②③ B. 仅有①② C. 仅有①③ D. 仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
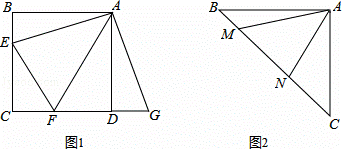
(1)如图,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
九年级(1)班开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现,老师调查了全班50名学生在这次活动中做家务的时间,并将统计的时间(单位:小时)分成5组:
A.0.5≤x<1 B.1≤x<1.5 C.1.5≤x<2 D.2≤x<2.5 E.2.5≤x<3;并制成两幅不完整的统计图(如图):

请根据图中提供的信息,解答下列问题:
(1)这次活动中学生做家务时间的中位数所在的组是 ;
(2)补全频数分布直方图;
(3 )该班的小明同学这一周做家务2小时,他认为自己做家务的时间比班里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计知识说明理由.
)该班的小明同学这一周做家务2小时,他认为自己做家务的时间比班里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
在3月份,某县某一周七天的最高气温(单位:℃)分别为:12,9,10,6,11,12,17,则这组数据的极差是( )
|
| A. | 6 | B. | 11 | C. | 12 | D. | 17 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在下列叙述中:
①一组对边相等的四边形是平行四边形;
②函数y=中,y随x的增大而减小;
③有一组邻边相等的平行四边形是菱形;
④有不可能事件A发生的概率为0.0001.
正确的叙述有( )
|
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
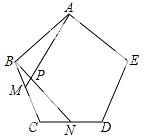
如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com