

分析 (1)由已知得顶点G(5,3),设抛物线为顶点式:y=a(x-5)2+3,把C(0,2)代入可得解析式;
(2)由排球场的长度OD为15米,中点A为(7.5,0),得出点F的横坐标为8,代入抛物线解析式后,与2.7比较可知结果;
(3)由题意可知当x=7.5时,y要大于2.5;当x=15时,y≤0;代入解析式列不等式组可得取值范围.
解答 解:(1)顶点G(5,3),
设y=a(x-5)2+3,
把C(0,2)代入得:2=a(0-5)2+3,
a=-$\frac{1}{25}$,
∴y=-$\frac{1}{25}$(x-5)2+3;
(2)由题意可知:OD=15,
∴OB=7.5,OF=7.5+0.5=8,
当x=8时,y=-$\frac{1}{25}$×(8-5)2+3=2.64<2.7,
∴这次她可以拦网成功;
(3)设y=a(x-5)2+h,
将C(0,2)代入y=a(x-5)2+h中,得:
a(0-5)2+h=2,a=$\frac{2-h}{25}$,
∴y=$\frac{2-h}{25}(x-5)^{2}+h$,
由$\left\{\begin{array}{l}{\frac{2-h}{25}(7.5-5)^{2}+h>2.5}\\{\frac{2-h}{25}(15-5)^{2}+h≤0}\end{array}\right.$,
解得h>$\frac{8}{3}$.
点评 本题是二次函数的应用,解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,本题的第三问是求范围的问题,可以利用临界点法确定变量x或y的取值,再根据题意确定范围.


科目:初中数学 来源: 题型:选择题
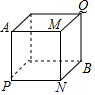 如图,一只蚂蚁沿边长为a的正方体表面从点A爬到点B,则它走过的路程最短为( )
如图,一只蚂蚁沿边长为a的正方体表面从点A爬到点B,则它走过的路程最短为( )| A. | $\sqrt{3}$a | B. | (1+$\sqrt{2}$)a | C. | 3a | D. | $\sqrt{5}$a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
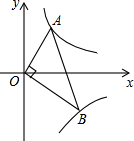 如图,已知点A,B分别在反比例函数y=$\frac{2}{x}$(x>0),y=$\frac{-8}{x}$(x>0)的图象上且OA⊥OB,则OA:OB为( )
如图,已知点A,B分别在反比例函数y=$\frac{2}{x}$(x>0),y=$\frac{-8}{x}$(x>0)的图象上且OA⊥OB,则OA:OB为( )| A. | $\frac{1}{\sqrt{2}}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{\sqrt{3}}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(元) | … | 35 | 40 | 45 | 50 | … |
| y(件) | … | 750 | 700 | 650 | 600 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
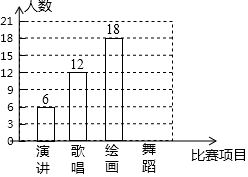 哈市某中学为了丰富校园文化生活,校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加,且只能参加其中一项比赛.围绕“你参赛的项目是什么?(必选且只选一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查,将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:4.请你根据以上信息回答下列问题:
哈市某中学为了丰富校园文化生活,校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加,且只能参加其中一项比赛.围绕“你参赛的项目是什么?(必选且只选一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查,将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:4.请你根据以上信息回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com