
【题目】四边形ABCD坐标为A(0,0),B(0,3),C(3,5),D(5,0).
(1)请在平面直角坐标系中画出四边形ABCD;
(2)把四边形ABCD先向上平移2个单位,再向左平移3个单位得到四边形![]() ,求平移后各顶点的坐标;
,求平移后各顶点的坐标;
(3)求四边形ABCD的面积.

【答案】(1)见解析;(2)四边形A1B1C1D1见解析,A1(-3,2),B1(-3,5),C1(0,7),D1(2,2);(3)17.
【解析】
(1)根据各点的坐标建立直角坐标系,然后描出各点并顺次连接即可;
(2)根据平移的规律:先向上平移2个单位,再向左平移3个单位,找出平移后各点的对应点,然后顺次连接各点,得到平移后的四边形A1B1C1D1,根据图形可直接写出平移后各顶点的坐标;
(3)利用分割法将四边形ABCD分为一个直角梯形和一个直角三角形,继而即可求出其面积.
解:(1)所画图形如下所示,四边形ABCD即为所求;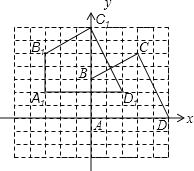
(2)平移后入得到的四边形A1B1C1D1如上图所示,
其中各顶点的坐标分别为:A1(-3,2),B1(-3,5),C1(0,7),D1(2,2);
(3)S四边形ABCD=![]() (3+5)×3+
(3+5)×3+![]() ×2×5=17.
×2×5=17.
故答案为:(1)见解析;(2)四边形A1B1C1D1见解析,A1(-3,2),B1(-3,5),C1(0,7),D1(2,2);(3)17.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在两建筑物之间有一根高15米的旗杆,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°.若旗杆底点G为BC的中点,则矮建筑物的高CD为( )
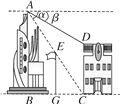
A. 20米 B. 10![]() 米 C. 15
米 C. 15![]() 米 D. 5
米 D. 5![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴、y轴的交点分别为A、![]() ,将
,将![]() 对折,使点O的对应点H恰好落在直线AB上,折痕交x轴于点C,
对折,使点O的对应点H恰好落在直线AB上,折痕交x轴于点C,
![]() 求过A、B、C三点的抛物线解析式;
求过A、B、C三点的抛物线解析式;
![]() 若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
![]() 若点Q是抛物线上一个动点,使得以A、B、Q为顶点并且以AB为直角边的直角三角形,直接写出Q点坐标.
若点Q是抛物线上一个动点,使得以A、B、Q为顶点并且以AB为直角边的直角三角形,直接写出Q点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A-B-C-D-A…循环爬行,其中A点坐标为(1,-1),B点坐标为(-1,-1),C点坐标为(-1,3),D点坐标为(1,3),当蚂蚁爬了2 018个单位长度时,它所处位置的坐标为_____________.
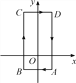
查看答案和解析>>
科目:初中数学 来源: 题型:
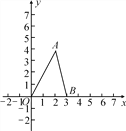
【题目】如图,在平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(3,0).三角形AOB中任意一点P(x0,y0)经平移后的对应点为P1(x0+2,y0),并且点A,O,B的对应点分别为点D,E,F.
(1)指出平移的方向和距离;
(2)画出平移后的三角形DEF;
(3)求线段OA在平移过程中扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴只有一个公共点.
轴只有一个公共点.
(![]() )求
)求![]() 的值.
的值.
(![]() )怎样平移抛物线
)怎样平移抛物线![]() 就可以得到抛物线
就可以得到抛物线![]() ?请写出具体的平移方法.
?请写出具体的平移方法.
(![]() )若点
)若点![]() 和点
和点![]() 都在抛物线
都在抛物线![]() 上,且
上,且![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
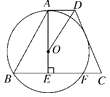
【题目】如图,梯形ABCD中,AD∥BC,AE⊥BC于点E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
(1)求证:CD与⊙O相切;
(2)若BF=24,OE=5,求tan∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=kx+b的图象与x轴、y轴分别交于点A(12,0),与函数y=x的图象交于点E,点E的横坐标为3.
(1)求函数y=kx+b的表达式;
(2)在x轴上有一点F(a,0),过点F作x轴的垂线,分别交函数y=kx+b的图象和函数y=x的图象于点C,D,若四边形OBDC是平行四边形,求a的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com