
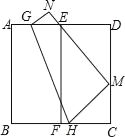
【题目】如图,将边长为3的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N,那么折痕GH的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
利用翻折变换的性质结合勾股定理表示出CH的长,得出△EDM∽△MCH,进而求出MC的长,依据△GPH≌△BCM,可得GH=BM,再利用勾股定理得出BM,即可得到GH的长.
设CM=x,设HC=y,则BH=HM=3﹣y,
故y2+x2=(3﹣y)2,
整理得:y=![]() ,
,
即CH=![]() ,
,
∵四边形ABCD为正方形,
∴∠B=∠C=∠D=90°,
由题意可得:ED=1.5,DM=3﹣x,∠EMH=∠B=90°,
故∠HMC+∠EMD=90°,
∵∠HMC+∠MHC=90°,
∴∠EMD=∠MHC,
∴△EDM∽△MCH,
∴ ![]() ,
,
即![]() ,
,
解得:x1=1,x2=3(不合题意),
∴CM=1,
如图,连接BM,过点G作GP⊥BC,垂足为P,则BM⊥GH,
∴∠PGH=∠HBM,
在△GPH和△BCM中
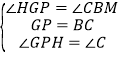 ,
,
∴△GPH≌△BCM(SAS),
∴GH=BM,
∴GH=BM=![]() .
.
故选:A.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】“才饮长沙水,又食武昌鱼”.因一代伟人毛泽东的佳句,“鄂州武昌鱼”名扬天下.某网店专门销售某种品牌真空包装的武昌鱼熟食产品,成本为30元/盒,每天销售y(盒)与销售单价x(元)之间存在一次函数关系,如图所示.
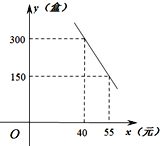
(1)求y与x之间的函数关系式;
(2)如果规定每天这种武昌鱼熟食产品的销售量不低于240盒,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3 600元,试确定这种武昌鱼熟食产品销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
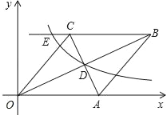
【题目】如图,在直角坐标系中有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于点D,双曲线y=![]() (x>0)经过点D,交BC的延长线于点E,且OBAC=160,则点E的坐标为_____.
(x>0)经过点D,交BC的延长线于点E,且OBAC=160,则点E的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22017
首先设S=1+2+22+23+24+…+22017 ① 则2S=2+22+23+24+25+…+22018 ②
②﹣①得S=22018﹣1 即1+2+22+23+24+…+22017=22018﹣1
以上解法,在数列求和中,我们称之为:“错位相减法”
请你根据上面的材料,解决下列问题
(1)求1+3+32+33+34+…+32019的值
(2)若a为正整数且![]() ,求
,求![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
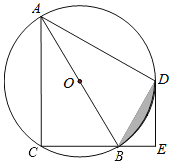
【题目】如图,四边形ACBD是⊙O的内接四边形,AB为直径,弧CD=弧AD,DE⊥BC,垂足为E.
(1)求证:BD平分∠ABE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若BE=2,AB=8,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
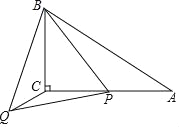
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点P是AC上的动点,连接BP,以BP为边作等边△BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
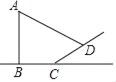
【题目】如图所示,小明准备测量学校旗杆AB的高度,他发现阳光下,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,测得水平地面上的影长BC=20m,斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成锐角为26°,斜坡CD与水平地面所成的锐角为30°,求旗杆AB的高度(精确到1m).(参考数据:sin26°=0.44,cos26°=0.90,tan26°=0.49)
查看答案和解析>>
科目:初中数学 来源: 题型:
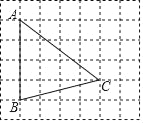
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)AC的长等于_____;
(Ⅱ)在线段AC上有一点D,满足AB2=ADAC,请在如图所示的网格中,用无刻度的直尺,画出点D,并简要说明点D的位置是如何找到的(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
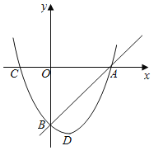
【题目】如图抛物线y=x2+bx-c经过直线y=x-3与坐标轴的两个交点A,B,与x轴交于另一点C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)求S△ACD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com