
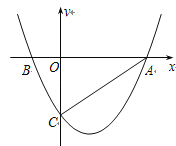
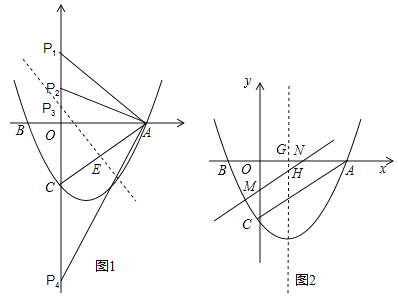
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,已知A(3,0),且M(1,
与x轴交于A、B两点,与y轴交于C点,已知A(3,0),且M(1,![]() )是抛物线上另一点.
)是抛物线上另一点.
(1)求a、b的值;
(2)连结AC,设点P是y轴上任一点,若以P、A、C三点为顶点的三角形是等腰三角形,求P点的坐标;
(3)若点N是x轴正半轴上且在抛物线内的一动点(不与O、A重合),过点N作NH∥AC交抛物线的对称轴于H点.设ON=t,△ONH的面积为S,求S与t之间的函数关系式.
【答案】(1)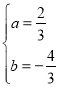 ;(2)P点的坐标1(0,2)或(0,
;(2)P点的坐标1(0,2)或(0,![]() )或(0,
)或(0,![]() )或(0,
)或(0,![]() );(3)
);(3)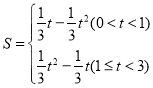 .
.
【解析】
试题分析:(1)根据题意列方程组即可得到结论;
(2)在![]() 中,当x=0时.y=﹣2,得到OC=2,如图,设P(0,m),则PC=m+2,OA=3,根据勾股定理得到AC=
中,当x=0时.y=﹣2,得到OC=2,如图,设P(0,m),则PC=m+2,OA=3,根据勾股定理得到AC=![]() =
=![]() ,①当PA=CA时,则OP1=OC=2,②当PC=CA=
,①当PA=CA时,则OP1=OC=2,②当PC=CA=![]() 时,③当PC=PA时,点P在AC的垂直平分线上,根据相似三角形的性质得到P3(0,
时,③当PC=PA时,点P在AC的垂直平分线上,根据相似三角形的性质得到P3(0,![]() ),④当PC=CA=
),④当PC=CA=![]() 时,于是得到结论;
时,于是得到结论;
(3)过H作HG⊥OA于G,设HN交Y轴于M,根据平行线分线段成比例定理得到OM=![]() ,求得抛物线的对称轴为直线x=
,求得抛物线的对称轴为直线x=![]() =
=![]() ,得到OG=
,得到OG=![]() ,求得GN=t﹣
,求得GN=t﹣![]() ,根据相似三角形的性质得到HG=
,根据相似三角形的性质得到HG=![]() ,于是得到结论.
,于是得到结论.
试题解析:(1)把A(3,0),且M(1,![]() )代入
)代入![]() 得:
得: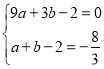 ,解得:
,解得: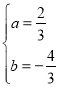 ;
;
(2)在![]() 中,当x=0时.y=﹣2,∴C(0,﹣2),∴OC=2,如图,设P(0,m),则PC=m+2,OA=3,AC=
中,当x=0时.y=﹣2,∴C(0,﹣2),∴OC=2,如图,设P(0,m),则PC=m+2,OA=3,AC=![]() =
=![]() ,分三种情况:
,分三种情况:
①当PA=CA时,则OP1=OC=2,∴P1(0,2);
②当PC=CA=![]() 时,即m+2=
时,即m+2=![]() ,∴m=
,∴m=![]() ﹣2,∴P2(0,
﹣2,∴P2(0,![]() ﹣2);
﹣2);
③当PC=PA时,点P在AC的垂直平分线上,则△AOC∽△P3EC,∴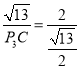 ,∴P3C=
,∴P3C=![]() ,∴m=
,∴m=![]() ,∴P3(0,
,∴P3(0,![]() ),④当PC=CA=
),④当PC=CA=![]() 时,m=﹣2﹣
时,m=﹣2﹣![]() ,∴P4(0,﹣2﹣
,∴P4(0,﹣2﹣![]() ),综上所述,P点的坐标1(0,2)或(0,
),综上所述,P点的坐标1(0,2)或(0,![]() )或(0,
)或(0,![]() )或(0,
)或(0,![]() );
);
(3)过H作HG⊥OA于G,设HN交Y轴于M,∵NH∥AC,∴![]() ,∴
,∴![]() ,∴OM=
,∴OM=![]() ,∵抛物线的对称轴为直线x=
,∵抛物线的对称轴为直线x=![]() =
=![]() ,∴OG=
,∴OG=![]() ,∴GN=t﹣
,∴GN=t﹣![]() ,∵GH∥OC,∴△NGH∽△NOM,∴
,∵GH∥OC,∴△NGH∽△NOM,∴![]() ,即
,即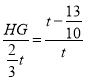 ,∴HG=
,∴HG=![]() ,∴S=
,∴S=![]() ONGH=
ONGH=![]() t(
t(![]() t﹣
t﹣![]() )=
)=![]() t2﹣
t2﹣![]() t(0<t<3).
t(0<t<3).
(3)设直线AC的解析式为y=kx+b(k≠0)由题意得:![]() ,解得:
,解得:![]() ,b=-2,∴
,b=-2,∴![]() .
.
由(1)得抛物线对应的函数表达式为![]() =
=![]() ,设AC与抛物线y=
,设AC与抛物线y=![]() 的对称轴x=1交于点F,直线x=1与x轴交于E点,则F(1,
的对称轴x=1交于点F,直线x=1与x轴交于E点,则F(1,![]() ),E(1,0).
),E(1,0).
①当0<t<1时,EN=1-t,由![]() 得,
得,![]() ,∴EH=
,∴EH=![]() ,∴
,∴![]() =
=![]() ONEH=
ONEH=![]() ,即
,即![]() ;
;
②当1≤t≤3时,EN=t-1,由![]() 得,
得,![]() ,∴EH=
,∴EH=![]() ,∴
,∴![]() =
=![]() ONEH=
ONEH=![]() ,即
,即![]() ;
;
∴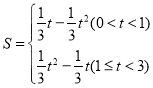 .
.


科目:初中数学 来源: 题型:
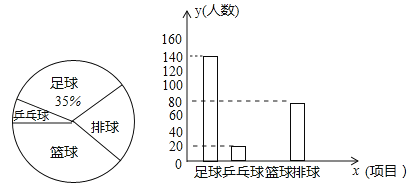
【题目】某校为提高学生身体素质,决定开展足球、篮球、台球、乒乓球四项课外体育活动,并要求学生必须并且只能选择一项.为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并绘制出以下两幅不完整的统计图.请根据统计图回答下列问题.(要求写出简要的解答过程)
(1)这次活动一共调查了多少名学生?
(2)补全条形统计图.
(3)若该学校总人数是1300人,请估计选择篮球项目的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠ABC=90°,点F为AB延长线上一点,点E在BC上,BE=BF,连接AE,EF和CF.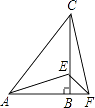
(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠EFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
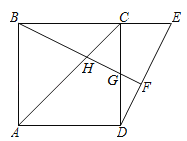
【题目】如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交BC于G.
(1)求证:BG=DE;
(2)若点G为CD的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
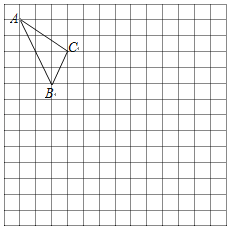
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A1B1C1;
(3)请在y轴上求作一点P,使△PB1C的周长最小,并写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
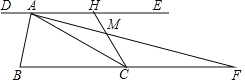
【题目】如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM=![]() AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是
AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是![]() ,则
,则![]() 的值是 .
的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大报告指出:“建设生态文明,是关系人民福祉、关乎民族未来的长远大计”,这些年党和政府在生态文明的发展进程上持续推进,在“十一五”期间,中国减少二氧化碳排放1 460 000 000吨,赢得国际社会广泛赞誉.将1 460 000 000用科学记数法表示为( )
A.146×107
B.1.46×107
C.1.46×109
D.1.46×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线 ![]() 与x轴相交于点A,与y轴相交于点B.
与x轴相交于点A,与y轴相交于点B.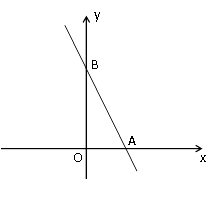
(1)直接写出A点的坐标;
(2)当x 时,y≤4;
(3)过B点作直线BP与x轴相交于P,若OP=2OA时,求ΔABP的面积。
(4)在y轴上是否存在E点,使得ΔABE为等腰三角形,若存在,直接写出满足条件的E点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com