
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°. 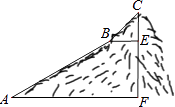
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.( ![]() 1.414,CF结果精确到米)
1.414,CF结果精确到米)
【答案】
(1)解:作BH⊥AF于H,如图,
在Rt△ABH中,∵sin∠BAH= ![]() ,
,
∴BH=800sin30°=400,
∴EF=BH=400m
(2)解:在Rt△CBE中,∵sin∠CBE= ![]() ,
,
∴CE=200sin45°=100 ![]() ≈141.4,
≈141.4,
∴CF=CE+EF=141.4+400≈541(m).
答:AB段山坡高度为400米,山CF的高度约为541米.
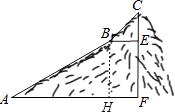
【解析】(1)作BH⊥AF于H,如图,在Rt△ABH中根据正弦的定义可计算出BH的长,从而得到EF的长;(2)先在Rt△CBE中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可.
【考点精析】根据题目的已知条件,利用关于坡度坡角问题的相关知识可以得到问题的答案,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用. 设每个房间每天的定价增加x元.求:
(1)房间每天的入住量y(间)关于x(元)的函数关系式;
(2)该宾馆每天的房间收费p(元)关于x(元)的函数关系式;
(3)该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x2+3x+2的图象如图1所示,根据图象回答问题: 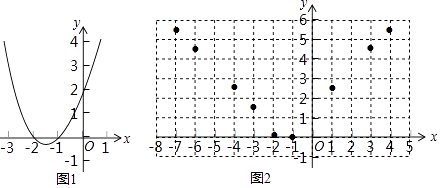
(1)当x时,x2+3x+2>0;
(2)在上述问题的基础上,探究解决新问题: ①函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
②如表是函数y= ![]() 的几组y与x的对应值.
的几组y与x的对应值.
x | … | ﹣7 | ﹣6 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 3 | 4 | … |
y | … | 5.477… | 4.472… | 2.449… | 1.414… | 0 | 0 | 1.414… | 2.449… | 4.472… | 5.477… | … |
如图2,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点的大概位置,请你根据描出的点,画出该函数的图象:
③写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为度(写出一个即可). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的速度沿折线A﹣B﹣C向点C运动,其中一点到达终点时,另一点也随之停止运动,设P,M两点运动的时间为t秒.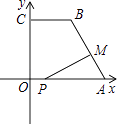
(1)求AB长;
(2)设△PAM的面积为S,当0≤t≤5时,求S与t的函数关系式,并指出S取最大值时,点P的位置;
(3)t为何值时,△APM为直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,请按要求完成下面的问题:
(1)以图中的点O为位似中心,将△ABC作位似变换且同向放大到原来的两倍,得到△A1B1C1;
(2)若△ABC内一点P的坐标为(a,b),则位似变化后对应的点P′的坐标是 . 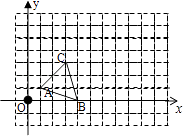
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点的坐标分别为(40,0)和(0,30),动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动、动直线EF从x轴开始以每1个单位的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于点E,F,连接EP,FP,设动点P与动直线EF同时出发,运动时间为t秒. 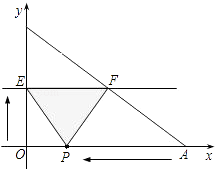
(1)求t=15时,△PEF的面积;
(2)直线EF、点P在运动过程中,是否存在这样的t,使得△PEF的面积等于160(平方单位)?若存在,请求出此时t的值;若不存在,请说明理由.
(3)当t为何值时,△EOP与△BOA相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4. 
(1)试在图中做出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),试在图中画出平面直角坐标系,并标出A、C两点的坐标;
(3)根据(2)的坐标系,以B为位似中心,做△BA2C2 , 使△BA2C2与△ABC位似,且△BA2C2与△ABC位似比为2:1,并直接写出A2的坐标. 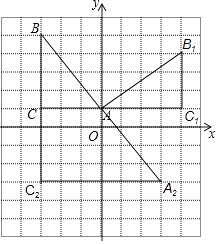
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com