
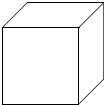
 某工厂要制作一个容积为300立方厘米的正方体形状的无盖水槽(如图所示).准备用钢板焊制,试求至少要用多少平方厘米的钢板?(结果精确到1平方厘米)
某工厂要制作一个容积为300立方厘米的正方体形状的无盖水槽(如图所示).准备用钢板焊制,试求至少要用多少平方厘米的钢板?(结果精确到1平方厘米) 科目:初中数学 来源: 题型:填空题
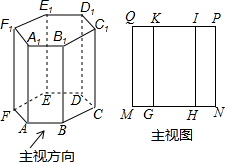 如图为一个几何体和它的主视图,请完成下面填空.
如图为一个几何体和它的主视图,请完成下面填空.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x+3y=z | B. | $\frac{4}{x}+y=5$ | C. | $y=\frac{1}{2}(x+8)$ | D. | x2-2x-3=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
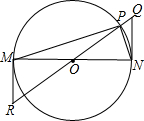 如图,过圆O直径的两端点M、N各引一条切线,在圆O上取一点P,过O、P两点的直线交两切线于R、Q.
如图,过圆O直径的两端点M、N各引一条切线,在圆O上取一点P,过O、P两点的直线交两切线于R、Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
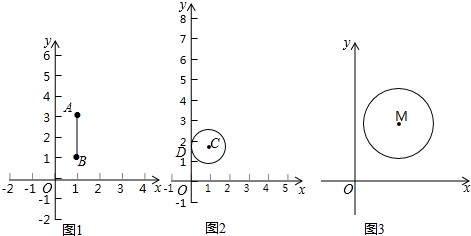
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com