
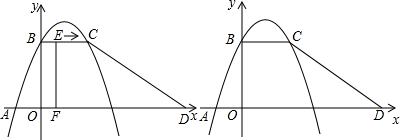
 、B1,设四边形A1B1EF与梯形ABCD重合部分的面积为S,F点的坐标是(x,0).
、B1,设四边形A1B1EF与梯形ABCD重合部分的面积为S,F点的坐标是(x,0).| OB |
| OA |
|
|
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |

| 1 |
| 2 |
| MA1 |
| NM |
| NM |
| MD |
| MN |
| A1M |
| 1 |
| 2 |
| CK |
| DK |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 14 |
| 3 |
| 1 |
| 3 |


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
 (2012•铁岭)如图,点E、F、G、H分别为菱形A1B1C1D1各边的中点,连接A1F、B1G、C1H、D1E得四边形A2B2C2D2,以此类推得四边形A3B3C3D3…,若菱形A1B1C1D1的面积为S,则四边形AnBnCnDn的面积为
(2012•铁岭)如图,点E、F、G、H分别为菱形A1B1C1D1各边的中点,连接A1F、B1G、C1H、D1E得四边形A2B2C2D2,以此类推得四边形A3B3C3D3…,若菱形A1B1C1D1的面积为S,则四边形AnBnCnDn的面积为| 1 |
| 5 |
| S |
| 5n-1 |
| 1 |
| 5 |
| S |
| 5n-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•铁岭)如图,AB为⊙O的直径,弦CD垂直平分OB于点E,点F在AB延长线上,∠AFC=30°.
(2012•铁岭)如图,AB为⊙O的直径,弦CD垂直平分OB于点E,点F在AB延长线上,∠AFC=30°.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•铁岭)如图,在斜坡AB上有一棵树BD,由于受台风影响而倾斜,恰好与坡面垂直,在地面上C点处测得树顶部D的仰角为60°,测得坡角∠BAE=30°,AB=6米,AC=4米.求树高BD的长是多少米?(结果保留根号)
(2012•铁岭)如图,在斜坡AB上有一棵树BD,由于受台风影响而倾斜,恰好与坡面垂直,在地面上C点处测得树顶部D的仰角为60°,测得坡角∠BAE=30°,AB=6米,AC=4米.求树高BD的长是多少米?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:
 -2x-1经过抛物线上一点B(-2,m)且与y轴交于点C,与抛物线的对称轴交于点F.
-2x-1经过抛物线上一点B(-2,m)且与y轴交于点C,与抛物线的对称轴交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com