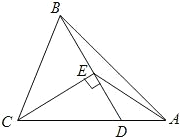
解:(1)BE=CF,理由为:
证明:∵BD为等边△ABC的中线,
∴BD⊥AC,即∠BDA=∠BDC=90°,
∵∠EDA=∠FDB,
∴∠EDA+∠BDA=∠FDB+∠BDC,即∠EDB=∠CDF,
由旋转的性质得到DE=DA=DC,BD=FD,
∵在△EDB和△CDF中,

,
∴△EDB≌△CDF(SAS),
∴BE=CF;
(2)α=60°或240°,
当α=60°时,由△ABC为等边三角形,得到∠A=60°,
∴∠A=∠EDA=60°,
∴ED∥AB;
当α=240°时,∠A=∠EDC=60°,
∴ED∥AB;
(3)不成立,添加的条件为AB=BC,
理由为:∵AB=BC,BD为中线,
∴BD⊥AC,即∠BDC=∠BDA=90°,DA=DC,
∵∠EDA=∠FDB,
∴∠EDA+∠BDA=∠FDB+∠BDC,即∠EDB=∠CDF,
由旋转的性质得到BD=FD,DA=DC=DE,
∵在△EDB和△CDF中,

,
∴△EDB≌△CDF(SAS),
∴BE=CF.
分析:(1)BE=CF,理由为:由BD为等边三角形ABC的中线,利用三线合一得到BD垂直于AC,得到一对直角相等,利用等式的性质得到一对角相等,再由旋转的性质及D为中点得到DE=DC,BD=FD,利用SAS得出三角形EBD与三角形CDF全等,利用全等三角形的对应边相等即可得证;
(2)由三角形ABC为等边三角形,利用等边三角形的性质得到∠A=60°,利用平行线的判定即可得出旋转角α的度数;
(3)若△ABC不是等边三角形时,(1)中结论不成立,需添加的条件为AB=BC,证明方法同(1).
点评:此题考查了等边三角形的性质,旋转的性质,以及全等三角形的判定与性质,熟练掌握等边三角形的性质是解本题的关键.

 在△ABC中,D为AC的中点,将△ABD绕点D顺时针旋转α°(0<α<360)得到△DEF,连接BE、CF.
在△ABC中,D为AC的中点,将△ABD绕点D顺时针旋转α°(0<α<360)得到△DEF,连接BE、CF. ,
, ,
,

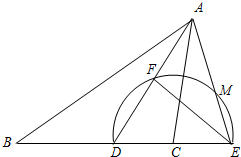 AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.
AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.