
①解分式方程![]() ;
;
②解不等式组![]() .
.
|
解:①去分母,得2(x-2)=3(x+2), 去括号,得2x-4=3x+6, 移项,得2x-3x=4+6, 解得x=-10, 检验:当x=-10时,(x+2)(x-2)≠0, ∴原方程的解为x=-10; ②不等式①化为x-2<6x+18, 解得x>-4, 不等式②化为5x-5-6≥4x+4, 解得x≥15, ∴不等式组的解集为x≥15. 分析:①公分母为(x+2)(x-2),去分母,转化为整式方程求解,结果要检验; ②先分别解每一个不等式,再求解集的公共部分,即为不等式组解. 点评:本题考查了分式方程,不等式组的解法.(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.解不等式组时,先解每一个不等式,再求解集的公共部分. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:阅读理解
| 2 |
| x |
| x |
| x-3 |
|
| 6 |
| 5 |
| 6 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 2 |
| x |
| x |
| x-3 |
|
| 6 |
| 5 |
| 6 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5ab |
| 3c |
| 12c2 |
| 5ab2 |
| 4c |
| b |
| 4c |
| b |
| x2 |
| x-y |
| y2 |
| y-x |
| 4 |
| a-2 |
| x2+6x+9 |
| x2-9 |
| x-3 |
| x+2 |
| x+3 |
| x |
| a-b |
| a |
| 2ab-b2 |
| a |
| x-4 |
| x-3 |
| 1 |
| 3-x |
| 3y-1 |
| y |
| 2y |
| y-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 2 |
| x+1 |
| 3 |
| x-1 |
| 1 |
| x2-1 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年河南省新密市兴华公学九年级3月第一次摸拟考试数学试卷(解析版) 题型:解答题
(1)解不等式组.并把解集在数轴上表示出来.
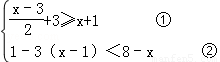 .
.
(2)阅读某同学解分式方程的具体过程,回答后面问题.
解方程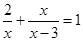 .
.
解:原方程可化为:
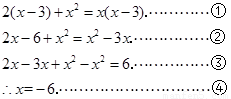
检验:当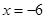 时,各分母均不为0,
时,各分母均不为0,
∴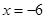 是原方程的解.
是原方程的解. ⑤
⑤
请回答:(1)第①步变形的依据是____________________;
(2)从第____步开始出现了错误,这一步错误的原因是__________________________;
(3)原方程的解为____________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com