
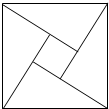
 如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的和等于10.
如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的和等于10. 分析 设两直角边分别为x,y,根据勾股定理求出大正方形的面积和小正方形的面积,列出方程组,解方程组求出两直角边长的和.
解答 解:设设三角形的两直角边分别为x,y,
则$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=52…①}\\{(x-y)^{2}=4…②}\end{array}\right.$,
由②得x2+y2-2xy=4…③,
①-③得2xy=48
则(x+y)2=x2+y2+2xy=52+48=100,
x+y=$\sqrt{100}$=10.
故答案是:10.
点评 此题主要考查了勾股定理和三角形,正方形的面积公式,解题关键在于找出各边关系列出方程.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (6,1) | B. | (0,1) | C. | (0,-3) | D. | (6,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | ±$\sqrt{3}$ | D. | ±3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com