
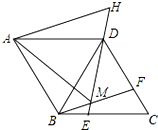
 如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:分析 根据菱形的四条边都相等,先判定△ABD是等边三角形,再根据菱形的性质可得∠BDF=∠C=60°,再求出DF=CE,然后利用“边角边”即可证明△BDF≌△DCE,从而判定①正确;根据全等三角形对应角相等可得∠DBF=∠EDC,然后利用三角形的一个外角等于与它不相邻的两个内角的和可以求出∠DMF=∠BDC=60°,再根据平角等于180°即可求出∠BMD=120°,从而判定④正确;根据三角形的一个外角等于与它不相邻的两个内角的和以及平行线的性质求出∠ABM=∠ADH,再利用“边角边”证明△ABM和△ADH全等,根据全等三角形对应边相等可得AH=AM,对应角相等可得∠BAM=∠DAH,然后求出∠MAH=∠BAD=60°,从而判定出△AMH是等边三角形,判定出③正确;根据全等三角形的面积相等可得△AMH的面积等于四边形ABMD的面积,然后判定出②错误
解答 解:在菱形ABCD中,
∵AB=BD,
∴AB=BD=AD,
∴△ABD是等边三角形,
∴根据菱形的性质可得∠BDF=∠C=60°,
∵BE=CF,
∴BC-BE=CD-CF,
即CE=DF,
在△BDF和△DCE中,$\left\{\begin{array}{l}{CE=DF}\\{∠BDF=∠C=60°}\\{BD=CD}\end{array}\right.$,
∴△BDF≌△DCE(SAS),故①小题正确;
∴∠DBF=∠EDC,
∵∠DMF=∠DBF+∠BDE=∠EDC+∠BDE=∠BDC=60°,
∴∠BMD=180°-∠DMF=180°-60°=120°,故④小题正确;
∵∠DEB=∠EDC+∠C=∠EDC+60°,∠ABM=∠ABD+∠DBF=∠DBF+60°,
∴∠DEB=∠ABM,
又∵AD∥BC,
∴∠ADH=∠DEB,
∴∠ADH=∠ABM,
在△ABM和△ADH中,$\left\{\begin{array}{l}{AB=AD}\\{∠ADH=∠ABM}\\{DH=BM}\end{array}\right.$,
∴△ABM≌△ADH(SAS),
∴AH=AM,∠BAM=∠DAH,
∴∠MAH=∠MAD+∠DAH=∠MAD+∠BAM=∠BAD=60°,
∴△AMH是等边三角形,故③小题正确;
∵△ABM≌△ADH,
∴△AMH的面积等于四边形ABMD的面积,
又∵△AMH的面积=$\frac{1}{2}$AM•$\frac{\sqrt{3}}{2}$AM=$\frac{\sqrt{3}}{4}$AM2,
∴S四边形ABMD=$\frac{\sqrt{3}}{4}$AM2,故②小题错误,
综上所述,正确的是①③④,
故答案为:①③④
点评 本题考查了菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质,题目较为复杂,特别是图形的识别有难度,从图形中准确确定出全等三角形并找出全等的条件是解题的关键.


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:填空题
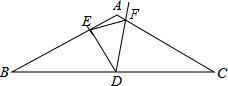 已知:△ABC中,AB=AC,∠BAC=120°,D为BC的中点,且∠EDF=∠C.
已知:△ABC中,AB=AC,∠BAC=120°,D为BC的中点,且∠EDF=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
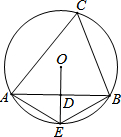 如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论①AB⊥DE;②AE=BE;③OD=DE;④∠AEO=∠C;⑤$\widehat{AE}$=$\frac{1}{2}$$\widehat{AEB}$.正确结论的个数是( )
如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论①AB⊥DE;②AE=BE;③OD=DE;④∠AEO=∠C;⑤$\widehat{AE}$=$\frac{1}{2}$$\widehat{AEB}$.正确结论的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
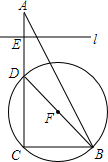 如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,D、E两点分别从顶点C、A沿着AC边向点A、C运动,点D的速度为1个单位/秒,点E的速度为2个单位/秒.以BD为直径作⊙F,过点E作CB边的平行线l,问$\frac{10-\sqrt{10}}{6}$秒钟后直线l与⊙F相切.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,D、E两点分别从顶点C、A沿着AC边向点A、C运动,点D的速度为1个单位/秒,点E的速度为2个单位/秒.以BD为直径作⊙F,过点E作CB边的平行线l,问$\frac{10-\sqrt{10}}{6}$秒钟后直线l与⊙F相切.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$x | B. | -$\frac{1}{x}$ | C. | $\frac{1}{x}$ | D. | -$\frac{x-2}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com