某海产品市场管理部门规划建造面积为2400m2的集贸大棚,大棚内设A种类型和B种类型的店面共80间,每间A种类型的店面的平均面积为28m2,月租费为400元;每间B种类型的店面的平均面积为20m2,月租费为360元.全部店面的建造面积不低于大棚总面积的80%,又不能超过大棚总面积的85%.
(1)试确定A种类型店面的数量的范围;
(2)该大棚管理部门通过了解业主的租赁意向得知,A种类型店面的出租率为75%,B种类型店面的出租率为90%.
①开发商计划每年能有28万元的租金收入,你认为这一目标能实现吗?若能,应该如何安排A、B两类店面数量?若不能,说明理由.
②为使店面的月租费最高,最高月租金是多少?
解:(1)设A型店面x间,则
2400×80%≤28x+20(80-x)≤2400×85%
解得,40≤x≤55.
(2)①令12×400×75%x+12×360(80-x)×90%=280000
则x=
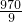
,x不是整数
所以,目标不能实现.
②设月租费为W元,则
W=400×75%x+360(80-x)×90%=-24X+25920
由于W随着x的增大而减小,故当x=40时W最大,为24960元.
分析:(1)设A型店面x间,则根据“全部店面的建造面积不低于大棚总面积的80%”“不能超过大棚总面积的85%”列不等式求解即可得到40≤x≤55;
(2)根据“每年能有28万元的租金收入”作为相等关系列式解答即可.另外要考虑x的取值必须为整数;
(3)设月租费为W元,则W=400×75%x+360(80-x)×90%=-24X+25920,根据函数的单调性和自变量的取值范围可求得最值.
点评:本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.要会根据自变量的取值范围结合函数的单调性求函数的最值问题.

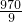 ,x不是整数
,x不是整数
