
【题目】列分式方程解应用题:
某商场销售某种商品,第一个月将此商品的进价加价20%作为销售价,共获利6000元。第二个月商场搞促销活动,将商品的进价加10%作为销售价,第二个月的销售量比第一个月增加了100件,并且商场第二个月比第一个月多获利2000元。问此商品进价是多少元?商场第二个月共销售多少件?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断

A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ABCD 是正方形,点 E,F 分别在 BC,CD 上,点 G 在 CD 的延长线上,且 BE=CF=DG 以线段AE,AG 为两邻边作 AEHG.
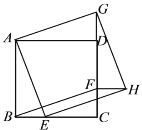
(1)求证:四边形 BEHF 是平行四边形.
(2)若四边形 ABCD 与 AEHG 的面积分别为 16,18.试求四边形 BEHF 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的不断提高,越来越多的人选择到电影院观看电影,体验视觉盛宴,并且更多的人通过网上平台购票,既快捷又能享受更多优惠.某电影城2019年从网上购买![]() 张电影票的费用比现场购买
张电影票的费用比现场购买![]() 张电影票的费用少
张电影票的费用少![]() 元:从网上购买
元:从网上购买![]() 张电影票的费用和现场购买
张电影票的费用和现场购买![]() 张电影票的费用共
张电影票的费用共![]() 元.
元.
(1)求该电影城2019年在网上购票和现场购票每张电影票的价格为多少元?
(2)2019年五一当天,该电影城按照2019年网上购票和现场购票的价格销售电影票,当天售出的总票数为![]() 张.五一假期过后,观影人数出现下降,于是电影城决定从5月5日开始调整票价:现场购票价格下调,网上购票价格不变,结果发现,现场购票每张电影票的价格每降低
张.五一假期过后,观影人数出现下降,于是电影城决定从5月5日开始调整票价:现场购票价格下调,网上购票价格不变,结果发现,现场购票每张电影票的价格每降低![]() 元,售出总票数就比五一当天增加
元,售出总票数就比五一当天增加![]() 张.经统计,5月5日售出的总票数中有
张.经统计,5月5日售出的总票数中有![]() 的电影票通过网上售出,其余通过现场售出,且当天票房总收入为
的电影票通过网上售出,其余通过现场售出,且当天票房总收入为![]() 元,试求出5月5日当天现场购票每张电影票的价格为多少元?
元,试求出5月5日当天现场购票每张电影票的价格为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
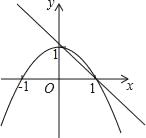
【题目】如图,已知抛物线y1=﹣x2+1,直线y2=﹣x+1,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=2时,y1=﹣3,y2=﹣1,y1<y2,此时M=﹣3.下列判断中:
①当x<0或x>1时,y1<y2;
②当x<0时,M=y1;
③使得M=![]() 的x的值是﹣
的x的值是﹣![]() 或
或![]() ;
;
④对任意x的值,式子![]() =1﹣M总成立.
=1﹣M总成立.
其中正确的是_____(填上所有正确的结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,下列说法不正确的是()。

A. △CDH的周长等于AD+CD B. FC平分∠BFD C. AC2+BF2=4CD2 D. DE2=EF.CE
查看答案和解析>>
科目:初中数学 来源: 题型:
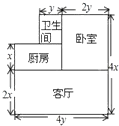
【题目】小李家住房结构如图所示,小李打算把卧室和客厅铺上木地板.
(1)请问他至少需要买多少平方米的木地板?(用字母表示)
(2)若![]() 米,
米,![]() 米时,并且每平方米木地板的价格是
米时,并且每平方米木地板的价格是![]() 元,则他至少需要准备多少元钱?
元,则他至少需要准备多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE、DE分别平分∠BAD、∠ADC,E点在BC上.
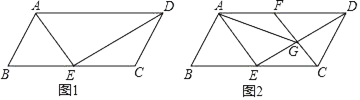
(1)求证:BC=2AB;
(2)若AB=3cm,∠B=60°,一动点F以1cm/s的速度从A点出发,沿线段AD运动,CF交DE于G,当CF∥AE时:
①求点F的运动时间t的值;②求线段AG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
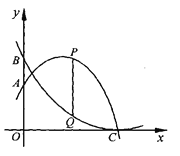
【题目】如图、点A、B分别为抛物线![]() 、
、![]() 与y轴交点,两条抛物线都经过点C(6,0)。点P、Q分别在抛物线
与y轴交点,两条抛物线都经过点C(6,0)。点P、Q分别在抛物线 ![]() 、
、![]() 上,点P在点Q的上方,PQ平行y轴,设点P的横坐标为m。
上,点P在点Q的上方,PQ平行y轴,设点P的横坐标为m。
(1)求b和c的值
(2)求以A、B、P、Q为顶点的四边形是平行四边形时m的值。
( 3 )当m为何值是,线段PQ的长度取的最大值?并求出这个最大值。
(4)直接写出线段PQ的长度随m增大而减小的m的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com