
【题目】如图,已知△ABC,AC<AB.
(1) 用直尺和圆规作出一条过点A的直线l,使得点C关于直线l的对称点落在边AB上(不写作法,保留作图痕迹);
(2) 设直线l与边BC的交点为D,且∠C=2∠B,请你通过观察或测量,猜想线段AB、AC、CD之间的数量关系,并说明理由.

【答案】(1)作图见解析;(2)AB=AC+CD.
【解析】试题分析:(1)先作∠BAC的平分线l,再过点C作CF⊥l交AB于F,则可得到点C和F点关于l对称,所以l为所作;
(2)连结DF,如图,利用等腰三角形的判定方法得到AF=AC,则AD垂直平分CF,所以DF=DC,则∠DCF=∠DFC,再利用三角形外角性质得∠BDF=2∠DCF,接着证明∠B=2∠BCF,于是得到∠B=∠BDF,则FB=FD=CD,则易得AB=AF+FB=AC+CD.
试题解析:(1)如图,直线l为所作;
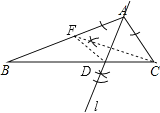
(2)AB=AC+CD.理由如下:
连结DF,如图,
∵AD平分∠BAC,AD⊥CF,
∴AF=AC,
∴AD垂直平分CF,
∴DF=DC,
∴∠DCF=∠DFC,
∴∠BDF=∠DCF+∠DFC=2∠DCF,
∵∠AFC=∠ACF,
∵∠AFC=∠B+∠BCF,
∴∠ACF=∠B+∠BCF,
∵∠ACB=2∠B,
∴2∠B-∠BCF=∠B+∠BCF,
∴∠B=2∠BCF,
∴∠B=∠BDF,
∴FB=FD,
∴FB=CD,
∴AB=AF+FB=AC+CD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(5,3),点C(0,8),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)求△ABC的面积;
(3)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班有60名学生,班长把全班学生对周末出游地的意向绘制成了扇形统计图,其中“想去重庆金佛山滑雪的学生数”的扇形圆心角是60°,则下列说法正确的是( )
A.想去重庆金佛山滑雪的学生有12人
B.想去重庆金佛山滑雪的学生肯定最多
C.想去重庆金佛山滑雪的学生占全班学生的 ![]()
D.想去重庆金佛山滑雪的学生占全班学生的60%
查看答案和解析>>
科目:初中数学 来源: 题型:
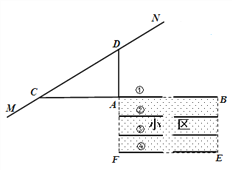
【题目】根据规定:距离高铁轨道 200米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.
如图是一个小区平面示意图,矩形ABEF为一新建小区,直线MN为高铁轨道,C、D是直线MN上的两点,点C、A、B在一直线上,且DA⊥CA,∠ACD=30°,AD=220.某人看中了①号楼A单元的一套住宅,但是感觉小区距离高铁轨道这么近,易受噪音污染,而售楼人员却说,虽然A单元离高铁轨道最近,但是AD长达220米,是达到设计要求的.
(1) 你认为售楼人员的话是否可信?为什么?
(2) 若一列长度为228米的高铁以70米/秒的速度通过时,则A单元用户受到影响时间有多长?(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7,
≈1.7, ![]() ≈61)
≈61)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形OAB的顶点O(0,0),A(0,6),将该三角形绕点O顺时针旋转,每次旋转60°,则旋转2017次后,顶点B的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分4个等级,将调查结果绘制成如下条形统计图和扇形统计图.根据图中信息,这些学生的平均分数是( ) 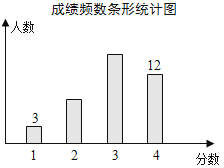

A.2.2
B.2.5
C.2.95
D.3.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com