
 如图,在平面直角坐标系中,已知点A(0,3$\sqrt{3}$),B(3,0),点C在线段AB上,且点C的横坐标为1.若点P为y轴上的一个动点,则PC+PB的最小值是( )
如图,在平面直角坐标系中,已知点A(0,3$\sqrt{3}$),B(3,0),点C在线段AB上,且点C的横坐标为1.若点P为y轴上的一个动点,则PC+PB的最小值是( )| A. | 2$\sqrt{7}$ | B. | 4 | C. | 3$\sqrt{7}$ | D. | 1+2$\sqrt{7}$ |
分析 求出B点关于y轴的对称点B′,连接B′C,交y轴于点P,则P即为所求点,利用两点间的距离公式即可求解.
解答  解:设C的纵坐标为y,
解:设C的纵坐标为y,
∵点A(0,3$\sqrt{3}$),B(3,0),点C在线段AB上,且点C的横坐标为1,
∴$\frac{3\sqrt{3}-y}{3\sqrt{3}}$=$\frac{1}{3}$,
∴y=2$\sqrt{3}$,
∴C(1,2$\sqrt{3}$),
如图所示:作点B关于y轴的对称点B′(-3,0),连接B′C,交y轴于点P,则P即为所求点,即当三点在一条直线上时有最小值,
即PC+PB=B′C=$\sqrt{(-3-1)^{2}+(0-2\sqrt{3})^{2}}$=2$\sqrt{7}$.
故选A.
点评 本题题考查的是最短线路问题及两点间的距离公式,解答此题的关键是熟知两点之间线段最短的知识.


科目:初中数学 来源:2016-2017学年江西省下期九年级第一次月考数学试卷(解析版) 题型:解答题
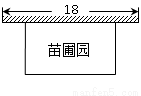
某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
 是一个完全平方式,则a的值为( )
是一个完全平方式,则a的值为( )
A. 4 B. 8 C. 4或-4 D. 8或-8
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
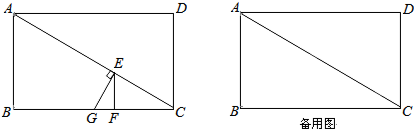
 气象台测得台风中心在A城正西方向600KM的B处,以每小时200KM的速度向北偏东60度BF方向移动,距离台风中心500KM的范围内是受台风影响的区域.
气象台测得台风中心在A城正西方向600KM的B处,以每小时200KM的速度向北偏东60度BF方向移动,距离台风中心500KM的范围内是受台风影响的区域.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com