
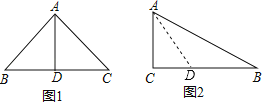
【题目】如图1,等边![]() 中,点
中,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,连
,连![]() 、
、![]() .
.

(1)求证:![]() ;
;
(2)如图2,延长![]() 至点
至点![]() ,使得
,使得![]() ,连
,连![]() ,试判断
,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)在(2)的条件下,连![]() ,
,![]() .若
.若![]() ,则
,则![]() ______.
______.
【答案】(1)详见解析;(2)![]()
【解析】
(1)先根据等边三角形的性质得出∠BAC=∠ACD=60°,AB=AC=BC,进而得出CD=AE,即可得出结论;
(2)先由△CAD≌△ABE,判断出∠CAD=∠ABE,进而得出∠AFE=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°,即可得出结论;
(3)先判断出∠BAF=∠CAG,进而判断出△ABF≌△ACG(SAS),得出∠AGC=∠AFB=180°-∠AFG=60°,判断出AD∥CG,即可得出结论.
解:(1)∵![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,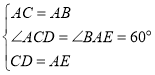 ,∴
,∴![]() ;
;
(2)由(1)知,![]() ,∴
,∴![]() ,
,
∴![]()
![]() ,
,
∵![]() ,∴
,∴![]() 是等边三角形;
是等边三角形;
(3)由(2)知,![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,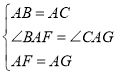 ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)请问EG与CG存在怎样的数量关系,并证明你的结论;
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
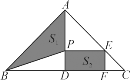
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC=16 cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以![]() cm/s的速度向点D运动,过P点作矩形PDFE(E点在AC上),设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8).
cm/s的速度向点D运动,过P点作矩形PDFE(E点在AC上),设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8).
(1)经过几秒钟后,S1=S2?
(2)经过几秒钟后,S1+S2最大?并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )
A. 1一定不是关于x的方程x2+bx+a=0的根
B. 0一定不是关于x的方程x2+bx+a=0的根
C. 1和﹣1都是关于x的方程x2+bx+a=0的根
D. 1和﹣1不都是关于x的方程x2+bx+a=0的根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:

(习题回顾)已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
(变式思考)如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
(探究廷伸)如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果经过三角形一个顶点的线段把这个三角形分成两个小三角形,其中一个三角形是等腰三角形,另外一个三角形和原三角形的三个内角分别相等,那么这条线段称为原三角形的“和谐分割线”,例如:如图1,等腰直角三角形斜边上的中线就是一条“和谐分割线”.
(1)判断(对的打“√”,错的打“×”)
①等边三角形存在“和谐分割线”( )
②如果三角形中有一个角是另一个角的两倍,则这个三角形必存在“和谐分割线”( )
(2)如图2,Rt△ABC,∠C=90°,∠B=30°,BC=6,请用尺规画出“和谐分割线”,并计算“和谐分割线”的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第100个图形中等边三角形的个数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC中,D、E分别是AB、AC的中点,延长BC至点F,使CF =![]() BC,连接DE、CD、EF.
BC,连接DE、CD、EF.

(1)求证:四边形DCFE是平行四边形;
(2)若等边三角形ABC的边长为a,写出求EF长的思路.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com