
����Ŀ��Ϊ���˽�������ѧ��ϲ���������������ȡ��������ķ�����������ƹ��������������ĸ����������ȫ��ѧ������Ȥ���ã����ݵ���Ľ�����Ƴ���ͼ��ʾ��������������ͳ��ͼ����ͼ��������Ҫ��ÿλѧ��ֻ��ѡ��һ���Լ�ϲ�������ࣩ���������ͼ���ṩ����Ϣ����������⣺
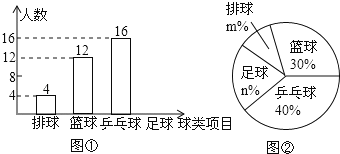
��1�����ι������ѧ������Ϊ___����������ͳ��ͼ����������
��2������ͳ��ͼ��m=___��n=___��
��3����ʾ�������������ε�Բ�Ľ���___�ȣ�
��4��������������ѧ������60000�ˣ���ϲ��ƹ������ж����ˣ�
���𰸡���1��40����ͼ����������2��10��20����3��72����4��24000�ˣ�
��������
��1������ϲ���������12�ˣ���ռ�İٷֱ���30%���ݴ˼��������������Ȼ��������������ȥ��������������ϲ���������������������ֱ��ͼ��
��2�����ݰٷֱȵ����弴����⣻
��3������360�����Զ�Ӧ�İٷֱȼ�����⣻
��4���������������Զ�Ӧ�İٷֱȼ�����⣮
�⣺��1��������������ǣ�12��30%=40���ˣ���
��ϲ������������ǣ�40-4-12-16=8���ˣ���
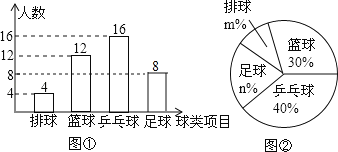 ��
��
�ʴ��ǣ�40��
��2��ϲ���������ռ�İٷֱ��ǣ�![]() ��100%=10%����m=10��
��100%=10%����m=10��
ϲ���������ռ�İٷֱ��ǣ�![]() ��100%=20%����n=20��
��100%=20%����n=20��
�ʴ�Ϊ��10��20��
��3����ʾ��������ε�Բ�Ľ��ǣ�360���20%=72����
�ʴ�Ϊ��72��
��4������������ѧ��ϲ��ƹ�������60000��40%=24000���ˣ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ��
��![]() ������
������![]() ��
��![]() ��Ĵ���
��Ĵ���![]() ����
����![]() ���߶�
���߶�![]() �ϣ�����
�ϣ�����![]() ���ӳ���ֱ��
���ӳ���ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() .
.
��1����![]() �Ķ�������ֱ��д��ֱ��
�Ķ�������ֱ��д��ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2������![]() �ĺ�����Ϊ2����
�ĺ�����Ϊ2����![]() �ij���
�ij���
��3����![]() ʱ�����
ʱ�����![]() ������.
������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������ֽƬABCD�ضԽ���BD�����۵�����C���ڵ�E����BE��AD�ڵ�F.
(1)��֤����BDF�ǵ��������Σ�
(2)��ͼ2������D��DG��BE����BC�ڵ�G������FG��BD�ڵ�O.
���ж��ı���BFDG����״����˵�����ɣ�
����AB��6��AD��8����FG�ij���
ͼ1

ͼ2

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ���y=��x2+4x+c��ͼ��A��1��y1����B����1��y2����C��2+ ![]() ��y3�����㣬��y1��y2��y3�Ĵ�С��ϵ�ǣ� ��
��y3�����㣬��y1��y2��y3�Ĵ�С��ϵ�ǣ� ��
A.y1��y2��y3
B.y1��y3��y2
C.y2��y3��y1
D.y2��y1��y3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ�����ǰ��ֱ�Ƕ���O�غ���һ������BOC��![]() ��AOD�����BOC�Ķ���Ϊ��������
��AOD�����BOC�Ķ���Ϊ��������
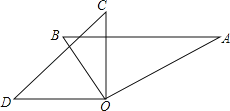
A.22.5��B.30��C.45��D.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������y=ax2+bx��3��x�ύ��A����1��0����B��3��0�����㣬��y�ύ�ڵ�C��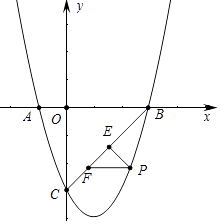
��1���������ߵĽ���ʽ��
��2����ͼ��ʾ��ֱ��BC�·�������������һ��P������p��PE��BC�ڵ�E����PFƽ����x�ύֱ��BC�ڵ�F�����PEF�ܳ������ֵ��
��3����֪��M�������ߵĶ��㣬��N��y����һ�㣬��Q������ƽ����һ�㣬����P����������һ�㣬��λ�������ߵĶԳ����Ҳ࣬�Ƿ������P��M��N��QΪ��������PMΪ�ߵ������Σ������ڣ�ֱ��д����P�ĺ����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ƻ���3 800Ԫ�������ܵ�120ֻ�������ֽ��ܵƵĽ��ۡ��ۼ����±���
����(Ԫ/ֻ) | �ۼ�(Ԫ/ֻ) | |
���� | 25 | 30 |
���� | 45 | 60 |
(1)��ס������ֽ��ܵƸ�������ֻ��
(2)ȫ������120ֻ���ܵƺ��̳����������Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com