
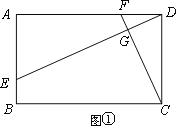
【题目】已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证![]() ;
;


(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得![]() 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图③,若BA=BC=4,DA=DC=6,∠BAD=90°,DE⊥CF,请直接写出![]() 的值.
的值.
【答案】(1)(2)见解析;(3)![]()
【解析】分析:(1)根据矩形性质得出∠A=∠FDC=90°,求出∠CFD=∠AED,证出△AED∽△DFC即可;
(2)当∠B+∠EGC=180°时,![]() 成立,证△DFG∽△DEA,得出
成立,证△DFG∽△DEA,得出![]() ,证△CGD∽△CDF,得出
,证△CGD∽△CDF,得出![]() ,即可得出答案;
,即可得出答案;
(3)过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,△BAD≌△BCD,推出∠BCD=∠A=90°,证△BCM∽△DCN,求出CM=![]() ,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,代入得出方程(x-4)2+(
,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,代入得出方程(x-4)2+(![]() )2=42,求出CN=
)2=42,求出CN=![]() ,证出△AED∽△NFC,即可得出答案.
,证出△AED∽△NFC,即可得出答案.
(1)证明:∵四边形ABCD是矩形,∴∠A=∠ADC=90°.
∴∠ADE+∠CDE=90°.
∵DE⊥CF,∴∠DCF+∠CDE=90°.
∴∠ADE=∠DCF.
∴△ADE∽△DCF,∴![]() .
.
(2)当∠B+∠EGC=180°时,![]() 成立.
成立.
证明如下:在AD的延长线上取点M,使CM=CF,则∠CMF=∠CFM.
∵AB∥CD,AD∥BC,∴∠A=∠CDM. ,∠CFM=∠FCB.
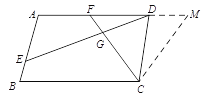
∵∠B+∠EGC=180°,∴∠FCB+∠BEG=180°.
∵∠AED+∠BEG=180°,∴∠AED=∠FCB.
∴∠CMF=∠AED.
∴△ADE∽△DCM.
∴![]() .即
.即![]() .
.
(3)![]() .
.
过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,
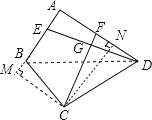
∵∠BAD=90°,即AB⊥AD,
∴∠A=∠M=∠CNA=90°,
∴四边形AMCN是矩形,
∴AM=CN,AN=CM,
∵在△BAD和△BCD中,
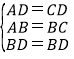
∴△BAD≌△BCD(SSS),
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC+∠CBM=180°,
∴∠MBC=∠ADC,
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
∴![]() ,
,
∴![]() ,
,
∴CM=![]() ,
,
在Rt△CMB中,CM=![]() ,BM=AM-AB=x-4,由勾股定理得:BM2+CM2=BC2,
,BM=AM-AB=x-4,由勾股定理得:BM2+CM2=BC2,
∴(x-4)2+(![]() )2=42,
)2=42,
x=0(舍去),x=![]() ,
,
CN=![]() ,
,
∵∠A=∠FGD=90°,
∴∠AED+∠AFG=180°,
∵∠AFG+∠NFC=180°,
∴∠AED=∠CFN,
∵∠A=∠CNF=90°,
∴△AED∽△NFC,
∴![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售,当此农产品售价为每袋36元时,3月份销售125袋,4、5月份该农产品十分畅销,销售量持续走高.在售价不变的基础上,5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.
(1)求4、5这两个月销售量的月平均增长率;
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/袋,销量就增加4袋,当农产品每袋降价多少元时,该商店6月份获利1920元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=1cm
(1)求AC的长
(2)若点E在直线AD上,且EA=2cm,求BE的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,△AOB中,∠AOB=90°,OA=OB,A(3,2),AB交 x轴于 C点
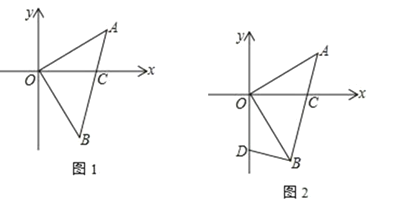
(1) 求△AOB的面积
(2) 如图2,点 D(0,![]() )在 y轴上,连 BD,求证:BD⊥AB
)在 y轴上,连 BD,求证:BD⊥AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC.MN是过点A的直线,BD⊥MN 于D,CE⊥MN于E.
(1)求证:BD=AE.
(2)若将MN绕点A旋转,使MN与BC相交于点G(如图2),其他条件不变,求证:BD=AE.
(3)在(2)的情况下,若CE的延长线过AB的中点F(如图3),连接GF,求证:∠AFE=∠BFG.
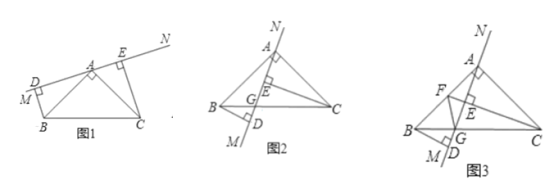
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图1为一个正方体,其棱长为12,图2为图1的表面展开图(数字和字母写在外面),请根据要求回答问题:
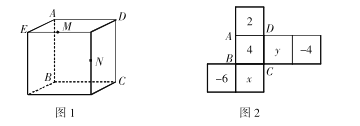
(1)若正方体相对面上的数互为相反数,则![]() _________;
_________;
(2)用一个平面去截这个正方体,下列关于截面(截出的面)的形状的结论:①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.其中所有正确结论的序号是( );
A.①② B.①④ C.①②④ D.①②③④
(3)图1中,![]() 为所在棱的中点,请在图2标出点
为所在棱的中点,请在图2标出点![]() 的位置,并求出
的位置,并求出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠EOC=2∠AOE.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=54°,求∠EOC的度数.
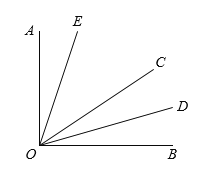
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com