
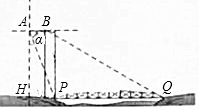
 如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的分析 ①在Rt△AHP中,由tan∠APH=tanα=$\frac{AH}{HP}$,即可解决问题;
②设BC⊥HQ于C.在Rt△BCQ中,求出CQ=$\frac{BC}{tan30°}$=1500米,由PQ=1255米,可得CP=245米,再根据AB=HC=PH-PC计算即可;
解答 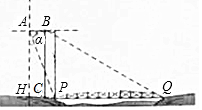 解:①在Rt△AHP中,∵AH=500$\sqrt{3}$,
解:①在Rt△AHP中,∵AH=500$\sqrt{3}$,
由tan∠APH=tanα=$\frac{AH}{HP}$=$\frac{500\sqrt{3}}{PH}$=2$\sqrt{3}$,可得PH=250米.
∴点H到桥左端点P的距离为250米.
②设BC⊥HQ于C.
在Rt△BCQ中,∵BC=AH=500$\sqrt{3}$,∠BQC=30°,
∴CQ=$\frac{BC}{tan30°}$=1500米,
∵PQ=1255米,
∴CP=245米,
∵HP=250米,
∴AB=HC=250-245=5米.
答:这架无人机的长度AB为5米.
点评 本题考查解直角三角形-仰角俯角问题,锐角三角函数,矩形判定和性质等知识,解题的关键是灵活应用所学知识解决问题,属于中考常考题型.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:选择题
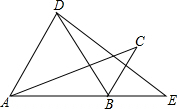 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )
如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )| A. | ∠ABD=∠E | B. | ∠CBE=∠C | C. | AD∥BC | D. | AD=BC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 研发组 | 管理组 | 操作组 | |
| 日工资(元) | 200 | 180 | 160 |
| 人数(人) | 3 | 4 | 5 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
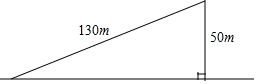 如图,一个斜坡长130m,坡顶离水平地面的距离为50m,那么这个斜坡与水平地面夹角的正切值等于( )
如图,一个斜坡长130m,坡顶离水平地面的距离为50m,那么这个斜坡与水平地面夹角的正切值等于( )| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{5}{12}$ | D. | $\frac{13}{12}$ |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年山东省新泰市六年级(五四学制)下学期第一次月考数学试卷(解析版) 题型:填空题
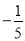 xa-1y与-3x2yb+3是同类项,则a+3b=__________.
xa-1y与-3x2yb+3是同类项,则a+3b=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com