
【题目】如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠AOC和∠COB的度数. 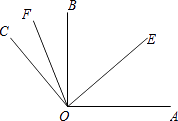
【答案】解:∵OE平分∠AOB,OF平分∠BOC, ∴∠BOE= ![]() ∠AOB=
∠AOB= ![]() ×90°=45°,∠COF=∠BOF=
×90°=45°,∠COF=∠BOF= ![]() ∠BOC,
∠BOC,
∵∠BOF=∠EOF﹣∠BOE=60°﹣45°=15°,
∴∠BOC=2∠BOF=30°;
∠AOC=∠BOC+∠AOB=30°+90°=120°
【解析】根据角平分线的定义得到∠BOE= ![]() ∠AOB=45°,∠COF=∠BOF=
∠AOB=45°,∠COF=∠BOF= ![]() ∠BOC,再计算出∠BOF=∠EOF﹣∠BOE=15°,然后根据∠BOC=2∠BOF,∠AOC=∠BOC+∠AOB进行计算.
∠BOC,再计算出∠BOF=∠EOF﹣∠BOE=15°,然后根据∠BOC=2∠BOF,∠AOC=∠BOC+∠AOB进行计算.
【考点精析】利用角的平分线对题目进行判断即可得到答案,需要熟知从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.


科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2k﹣3)x+k2+1=0有两个不相等的实数根x1、x2.
(1)求k的取值范围;
(2)若x1、x2满足|x1|+|x2|=2|x1x2|﹣3,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大双,小双的妈妈申购到一张北京奥运会的门票,兄弟俩决定分别用标有数字且除数字以外没有其它任何区别的小球,各自设计一种游戏确定谁去.
大双:A袋中放着分别标有数字1,2,3的三个小球,B袋中放着分别标有数字4,5的两个小球,且都已各自搅匀,小双蒙上眼睛从两个口袋中各取出1个小球,若两个小球上的数字之积为偶数,则大双得到门票;若积为奇数,则小双得到门票.
小双:口袋中放着分别标有数字1,2,3的三个小球,且已搅匀,大双,小双各蒙上眼睛有放回地摸1次,大双摸到偶数就记2分,摸到奇数记0分;小双摸到奇数就记1分,摸到偶数记0分,积分多的就得到门票.(若积分相同,则重复第二次.)
(1)大双设计的游戏方案对双方是否公平?请你运用列表或树状图说明理由;
(2)小双设计的游戏方案对双方是否公平?不必说理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连结BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),将两块直角三角板的直角顶点C叠放在一起. 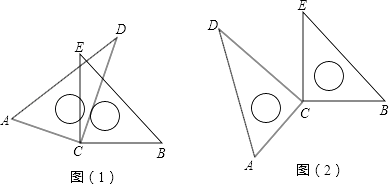
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校体育课进行定点投篮比赛,10位同学参加,每人连续投5次,投中情况统计如下:
投中球数量(个) | 2 | 3 | 4 | 5 |
人数(人) | 1 | 4 | 3 | 2 |
这10位同学投中球数量的众数和中位数分别是( )
A. 4, 2 B. 3,4 C. 2,3.5 D. 3,3.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com