
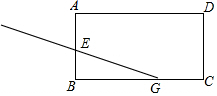
 如图,在矩形ABCD中,BG=10,BC=13,将纸片沿过点G的折痕GE折叠,使顶点B的对称点F落在边AD上,折痕与矩形的边交于点E,若满足条件的F点有2个时,AB的取值范围$\sqrt{91}$≤AB<10..
如图,在矩形ABCD中,BG=10,BC=13,将纸片沿过点G的折痕GE折叠,使顶点B的对称点F落在边AD上,折痕与矩形的边交于点E,若满足条件的F点有2个时,AB的取值范围$\sqrt{91}$≤AB<10.. 分析 如图1中,当点B′与点D重合时,求出AB的长,如图2中,当B′在AD上,BG′⊥AD时,AB=GB′=BG=10,几何图形即可解决问题.
解答 解:如图1中,当点B′与点D重合时,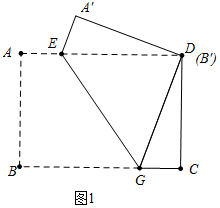
在Rt△CDG中,∵CD=10,CG=3,
∴AB=CD=$\sqrt{1{0}^{2}-{3}^{2}}$=$\sqrt{91}$,
如图2中,当B′在AD上,BG′⊥AD时,AB=GB′=BG=10,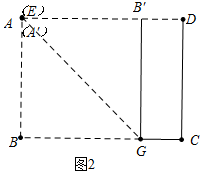
由图象可知,满足条件的F点有2个时,AB的取值范围是$\sqrt{91}$≤AB<10.
故答案为$\sqrt{91}$≤AB<10.
点评 本题考查矩形的性质、翻折变换、勾股定理等知识,解题的关键是学会寻找特殊点解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A、B、C是数轴上的三个点,它们分别表示三个数是a、b、c,其中b=1.
如图,A、B、C是数轴上的三个点,它们分别表示三个数是a、b、c,其中b=1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
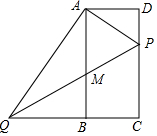 如图,在矩形ABCD中,点P在边CD上,与点C、D不重合,过点A作AP的垂线与CB的延长线交于点Q,连接PQ,M为线段PQ中点
如图,在矩形ABCD中,点P在边CD上,与点C、D不重合,过点A作AP的垂线与CB的延长线交于点Q,连接PQ,M为线段PQ中点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com