
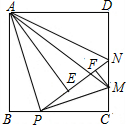
 ČēĶ¼£¬ŌŚ±ß³¤ĪŖ4µÄÕż·½ŠĪABCDÖŠ£¬PŹĒBC±ßÉĻŅ»¶Æµć£Ø²»ÓėB”¢CĮ½µćÖŲŗĻ£©£¬½«”÷ABPŃŲÖ±ĻßAP·ÕŪ£¬µćBĀäŌŚµćE“¦£»ŌŚCDÉĻČ”Ņ»µćM£¬Ź¹µĆ½«”÷CMPŃŲÖ±ĻßMP·ÕŪŗ󣬵ćCĀäŌŚÖ±ĻßPEÉĻµÄµćF“¦£¬Ö±ĻßPE½»CDÓŚµćN£¬Į¬½ÓAM”¢AN£®
ČēĶ¼£¬ŌŚ±ß³¤ĪŖ4µÄÕż·½ŠĪABCDÖŠ£¬PŹĒBC±ßÉĻŅ»¶Æµć£Ø²»ÓėB”¢CĮ½µćÖŲŗĻ£©£¬½«”÷ABPŃŲÖ±ĻßAP·ÕŪ£¬µćBĀäŌŚµćE“¦£»ŌŚCDÉĻČ”Ņ»µćM£¬Ź¹µĆ½«”÷CMPŃŲÖ±ĻßMP·ÕŪŗ󣬵ćCĀäŌŚÖ±ĻßPEÉĻµÄµćF“¦£¬Ö±ĻßPE½»CDÓŚµćN£¬Į¬½ÓAM”¢AN£®·ÖĪö £Ø1£©øł¾ŻÕż·½ŠĪµÄŠŌÖŹŗĶ¹“¹É¶ØĄķĒó³öAP£¬øł¾ŻÕżĻŅµÄ¶ØŅåµĆµ½sin”ĻBAP=$\frac{\sqrt{5}}{5}$£¬øł¾ŻÕŪµžµÄŠŌÖŹÖ¤Ć÷”ĻCPM=”ĻBAP£¬µĆµ½“š°ø£»
£Ø2£©Ö¤Ć÷Rt”÷AEN”ÕRt”÷ADN£¬µĆµ½”ĻEAN=”ĻDAN£¬¼ĘĖć¼“æÉ£»
£Ø3£©ÉčPB=x£¬øł¾ŻĻąĖĘČż½ĒŠĪµÄŠŌÖŹĒó³öDM£¬øł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½µĆµ½¶ž“ĪŗÆŹżµÄ½āĪöŹ½£¬øł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹ¼ĘĖć¼“æÉ£®
½ā“š ½ā£ŗ£Ø1£©”ßÕż·½ŠĪABCDµÄ±ß³¤ĪŖ4£¬PĪŖBCµÄÖŠµć£¬
”ąBP=$\frac{1}{2}$PC=2£¬
”ąAP=$\sqrt{A{B}^{2}+B{P}^{2}}$=2$\sqrt{5}$£¬
”ąsin”ĻBAP=$\frac{2}{2\sqrt{5}}$=$\frac{\sqrt{5}}{5}$£¬
ÓÉÕŪµžµÄŠŌÖŹæÉÖŖ£¬”ĻBPA=”ĻEPA£¬”ĻCPM=”ĻFPM£¬
”ą”ĻAPM=$\frac{1}{2}$£Ø”ĻBPE+”ĻCPF£©=90”ć£¬
”ą”ĻBPA+”ĻCPM=90”ć£¬ÓÖ”ĻBPA+”ĻBAP=90”ć£¬
”ą”ĻCPM=”ĻBAP£¬
”ąsin”ĻCPM=sin”ĻBAP=$\frac{\sqrt{5}}{5}$£¬
¹Ź“š°øĪŖ£ŗ$\frac{\sqrt{5}}{5}$£»
£Ø2£©ÓÉÕŪµžµÄŠŌÖŹæÉÖŖ£¬”ĻAEP=”ĻB=90”ć£¬AE=AB£¬”ĻBAP=”ĻEAP£¬
”ąAE=AD£¬
ŌŚRt”÷AENŗĶRt”÷ADNÖŠ£¬
$\left\{\begin{array}{l}{AE=AD}\\{AN=AN}\end{array}\right.$£¬
”ąRt”÷AEN”ÕRt”÷ADN£¬
”ą”ĻEAN=”ĻDAN£¬
”ą”ĻPAN=$\frac{1}{2}$”ĻBAD=45”ć£»
£Ø3£©ÉčPB=x£¬ŌņPC=4-x£¬
”ß”ĻCPM=”ĻBAP£¬”ĻABP=”ĻPCM=90”ć£¬
”ą”÷ABP”×”÷PCM£¬
”ą$\frac{AB}{PC}$=$\frac{BP}{CM}$£¬¼“$\frac{4}{4-x}$=$\frac{x}{CM}$£¬
½āµĆ£¬CM=-$\frac{1}{4}$x2+x£¬
”ąDM=4-£Ø-$\frac{1}{4}$x2+x£©=$\frac{1}{4}$x2-x+4£¬
”ą”÷ADMµÄĆ껿=$\frac{1}{2}$”Į4”Į£Ø$\frac{1}{4}$x2-x+4£©=$\frac{1}{2}$£Øx-2£©2+6£¬
”ąµ±BP=2Ź±£¬”÷ADMµÄĆ껿“ęŌŚ×īŠ”Öµ6£®
µćĘĄ ±¾Ģāæ¼²éµÄŹĒÕż·½ŠĪµÄŠŌÖŹ”¢Č«µČČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢ĻąĖĘČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢·×Ŗ±ä»»µÄŠŌÖŹ£¬ÕĘĪÕČ«µČČż½ĒŠĪµÄÅŠ¶Ø¶ØĄķ”¢ŠŌÖŹ¶ØĄķŗĶĻąĖĘČż½ĒŠĪµÄÅŠ¶Ø¶ØĄķ”¢ŠŌÖŹ¶ØĄķŅŌ¼°¶ž“ĪŗÆŹżµÄŠŌÖŹŹĒ½āĢāµÄ¹Ų¼ü£®


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -19 | B£® | -15 | C£® | -13 | D£® | -9 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | £Ø-2a£©•£Ø-a£©=2a2 | B£® | 3a2-6a2=-3 | C£® | 10a18+2a2=5a5 | D£® | -£Øa3£©2=a6 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com