练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

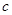    如图所示，在边长为的正方形中，有四个斜边为，直角边为的全等直角三角形，你能利用这个图说明勾股定理吗？写出理由。

     

    【答案】

    能,理由见解析

    【解析】本题考查的是勾股定理. 根据不同的方法计算大正方形的面积就可证明．

    解：能；

    ∵ab×4+（b-a）2=c2，

    ∴2ab+a2+b2-2ab=c2，

    ∴a2+b2=c2．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

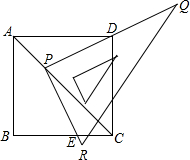    如图所示，在边长为1的正方形ABCD中，一直角三角尺PQR的直角顶点P在对角线AC上移动，直角边PQ经过点D，另一直角边与射线BC交于点E．
    （1）试判断PE与PD的大小关系，并证明你的结论；
    （2）连接PB，试证明：△PBE为等腰三角形．

    查看答案和解析>>

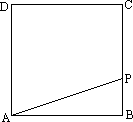
    科目：初中数学 来源：萧红中学(四年制)　新概念数学　八年级上(人教版) 题型：044

    如图所示，在边长为的正方形ABCD的一边BC上，有一点P从B点运动到C点．设PB＝x，图形APCD的面积为y，写出y与自变量x的函数关系式，并在直角坐标系系中画出它的图像．

    查看答案和解析>>

    科目：初中数学 来源：新课标　读想练同步测试　七年级数学(下) 北师大版 题型：044

    如图所示，在边长为的正方形ABCD的一边BC上，有一点P从点B运动到点C，设PB＝x，图形APCD的面积为y．

    (1)

    请写出y与x间的关系式；

    (2)

    当x＝1时，y等于多少？

    (3)

    当x＝0时，y等于多少？此时它表示的是什么？当x＝时，y等于多少？此时它表示的又是什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    如图所示，在边长为的正方形ABCD中，O为对角线交点，请作出正方形ABCD绕点O旋转45°后的图形，你能计算出这两个正方形重叠部分的面积吗？

    查看答案和解析>>

    同步练习册答案