
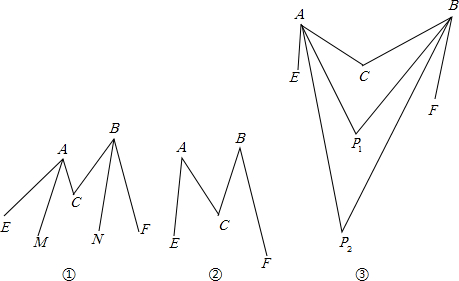
���� ��1�����ݽ�ƽ���ߵĶ����ʾ����MAC+��NCB���ٸ�����ֱ��ƽ�У��ڴ�����ȿɵá�C=��MAC+��NCB��
��2�����ݽ�ƽ���ߵĶ����ʾ����PAC+��PBC���ٷֵ�P�ڵ�C���·����Ϸ�������������������ε�һ����ǵ������������ڵ������ڽǵĺ���ʽ�������ɵý⣻
��3�����ݣ�2���Ľ��۷ֱ��ʾ����P1����P2�����Ӷ��ý⣮
���  �⣺��1����AM�ǡ�EAC��ƽ���ߣ�BN�ǡ�FBC��ƽ���ߣ�
�⣺��1����AM�ǡ�EAC��ƽ���ߣ�BN�ǡ�FBC��ƽ���ߣ�
���MAC+��NCB=$\frac{1}{2}$��EAC+$\frac{1}{2}$��FBC=$\frac{1}{2}$�£�
��AM��BN��
���C=��MAC+��NCB��
����=$\frac{1}{2}$�£�
��2���ߡ�EAC��ƽ�������FBCƽ�����ཻ��P��
���PAC+��PBC=$\frac{1}{2}$��EAC+$\frac{1}{2}$��FBC=$\frac{1}{2}$�£�
����P�ڵ�C���·������C=��APB+����PAC+��PBC����
����=��APB+$\frac{1}{2}$�£�
����P�ڵ�C���Ϸ������C+��APB=��PAC+��PBC��
����+��APB=$\frac{1}{2}$�£�
������������=��APB+$\frac{1}{2}$�»��+��APB=$\frac{1}{2}$�£�
��3���ɣ�2���ã���P1=��C-����PAC+��PBC��=��-$\frac{1}{2}$�£�
��P2=��P1-����P2AP1+��P2BP1����
=��-$\frac{1}{2}$��-$\frac{1}{4}$��=��-$\frac{3}{4}$�£�
��P3=��-$\frac{3}{4}$��-$\frac{1}{8}$��=��-$\frac{7}{8}$�£�
��P4=��-$\frac{7}{8}$��-$\frac{1}{16}$��=��-$\frac{15}{16}$�£�
��P5=��-$\frac{15}{16}$��-$\frac{1}{32}$��=��-$\frac{31}{32}$�£�
�ʴ�Ϊ����2����=��APB+$\frac{1}{2}$�»��+��APB=$\frac{1}{2}$�£���3����-$\frac{31}{32}$�£�
���� ���⿼����ƽ���ߵ����ʣ���ƽ���ߵĶ��壬�����ε�һ����ǵ������������ڵ������ڽǵĺ͵����ʣ�����˼��������ǽ���Ĺؼ���


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��һ����ѧ���ϣ�����ʦ�ںڰ��ϻ���ͼ����д�����ĸ���ʽ����AB=DC����BE=CE���ۡ�B=��C���ܡ�BAE=��CDE��Ҫ��ͬѧ�����ĸ���ʽ��ѡ��������Ϊ�������Ƴ���CAD=��BDA�����������������ʦ�����Ҫ��˵�����ɣ���д��һ�ּ��ɣ�
��һ����ѧ���ϣ�����ʦ�ںڰ��ϻ���ͼ����д�����ĸ���ʽ����AB=DC����BE=CE���ۡ�B=��C���ܡ�BAE=��CDE��Ҫ��ͬѧ�����ĸ���ʽ��ѡ��������Ϊ�������Ƴ���CAD=��BDA�����������������ʦ�����Ҫ��˵�����ɣ���д��һ�ּ��ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABD���ACE��Ϊ����ֱ���������Ұڳ���ͼ��ʾ�����ӣ�����ABC=90�㣨ͼ�����еĵ㡢�߶���ͬһƽ���ڣ���DF=$\sqrt{2}$��EF=2$\sqrt{2}$�����߶�BC�ij�Ϊ$\sqrt{7}$-1��
��ͼ����ABD���ACE��Ϊ����ֱ���������Ұڳ���ͼ��ʾ�����ӣ�����ABC=90�㣨ͼ�����еĵ㡢�߶���ͬһƽ���ڣ���DF=$\sqrt{2}$��EF=2$\sqrt{2}$�����߶�BC�ij�Ϊ$\sqrt{7}$-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com