
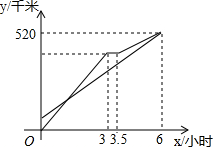
 甲、乙两车从A地出发沿同一路线驶向B地,甲车匀速驶向B地,甲车出发30分钟后,乙车才出发,乙先匀速行驶一段时间后,到达货站装货后继续行驶,速度减少了56千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法中正确的是( )
甲、乙两车从A地出发沿同一路线驶向B地,甲车匀速驶向B地,甲车出发30分钟后,乙车才出发,乙先匀速行驶一段时间后,到达货站装货后继续行驶,速度减少了56千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法中正确的是( )| A. | 甲车从A地到B地行驶了6小时 | |
| B. | 甲的速度是120千米/时 | |
| C. | 乙出发90分钟追上甲 | |
| D. | 当两车在行驶过程中,相距40千米时,x=2或3.5 |
分析 利用图中信息,先求出两人的速度,再寻找等量关系,列出方程,一一判断即可.
解答 解:A、错误.甲车从A地到B地行驶了6.5小时.
B、错误.甲的速度为$\frac{520}{6.5}$=80千米/时.
C、错误.设乙开始的速度为x千米/时,由题意3x+2.5(x-56)=520,解得x=120,
设乙出发t小时追上甲,则(120-80)t=0.5×80,t=1,
所以乙出发t小时追上甲.
D、正确.由题意甲的函数解析式为y=80x+40,
乙开始的函数解析式为y=120x,装货后的解析式为y=64x+136,
由题意120x-(80x+40)=40或64x+136-(80x+40)=40,
解得x=2或3.5.
故选D.
点评 本题考查一次函数的应用、行程问题的应用等知识,解题的关键是读懂图象信息,学会寻找等量关系列出方程解决问题,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
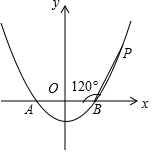 如图,已知抛物线y=ax2-4a(a>0)与x轴相交于A,B两点,点P是抛物线上一点,且PB=AB,∠PBA=120°.
如图,已知抛物线y=ax2-4a(a>0)与x轴相交于A,B两点,点P是抛物线上一点,且PB=AB,∠PBA=120°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:20170-(-$\frac{1}{3}$)-1
(1)计算:20170-(-$\frac{1}{3}$)-1查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
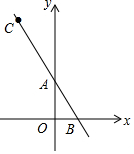 如图,过点C(-2,5)的直线AB分别交坐标轴于A(0,2),B两点,则tan∠OAB=( )
如图,过点C(-2,5)的直线AB分别交坐标轴于A(0,2),B两点,则tan∠OAB=( )| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com