
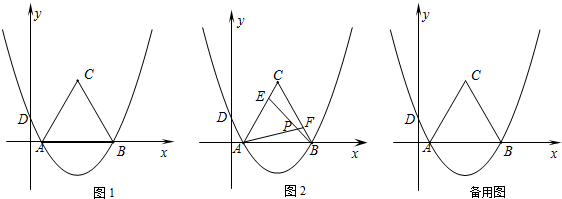
分析 (1)把A点和B点坐标代入y=-x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;然后利用待定系数法求直线AB的解析式;
(2)利用线段中点坐标公式求出C点坐标,再利用PC∥x轴可得到P点的纵坐标为$\frac{3}{2}$,然后根据二次函数图象上点的坐标特征确定P点坐标,再计算PC的长;
(3)设点P的坐标为(n,-n2+4n),利用四边形PCED为矩形可表示出C(s,-n2+4n),D(n,t),再利用点C、D在直线y=-x+4上得到-n2+4n=-s+4,t=-n+4,然后消去n得到s与t的函数关系式,再根据二次函数的性质确定s的范围.
解答 解:(1)∵点A(1,3),B(4,0)在抛物线y=-x2+bx+c上,
∴$\left\{\begin{array}{l}{-1+b+c=3}\\{-16+4b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=4}\\{c=0}\end{array}\right.$,
∴抛物线的解析式为y=-x2+4x;
∵点A(1,3),B(4,0)在直线y=kx+m上,
∴$\left\{\begin{array}{l}{k+m=3}\\{4k+m=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{m=4}\end{array}\right.$,
∴抛物线的解析式为y=-x+4;
(2)∵点C为线段AB的中点时,
∴C点坐标为($\frac{5}{2}$,$\frac{3}{2}$),
∵PC∥x轴,
∴P点的纵坐标为$\frac{3}{2}$,
当y=$\frac{3}{2}$时,-x2+4x=$\frac{3}{2}$,解得x1=2+$\frac{\sqrt{10}}{2}$(舍去),x2=2-$\frac{\sqrt{10}}{2}$,
∴P(2+$\frac{\sqrt{10}}{2}$,$\frac{3}{2}$),
∴PC=2+$\frac{\sqrt{10}}{2}$-$\frac{5}{2}$=$\frac{\sqrt{10}-1}{2}$;
(3)设点P的坐标为(n,-n2+4n),
∵四边形PCED为矩形,E(s,t),
∴C(s,-n2+4n),D(n,t),
而点C、D在直线y=-x+4上,
∴-n2+4n=-s+4,t=-n+4,即n=4-t,
∴-(4-t)2+4(4-t)=-s+4,
∴s=t2-4t+4(0<t<3),
∵s=(t-2)2,
∴抛物线的对称轴为直线t=2,
∵0<t<3时,当t=2时,s有最小值0,
而t=0时,s=4,
∴s的范围为0≤s<4.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和矩形的性质;会利用待定系数法求函数解析式;理解坐标与图形性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
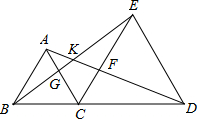 如图,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( )
如图,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
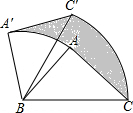 如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )
如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )| A. | π | B. | $\frac{3π}{2}$ | C. | $\frac{5π}{2}$ | D. | 3π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
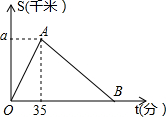 2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图象提供的信息,解答下列问题:
2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com