
����Ŀ�����Ķ����в��ϣ��������Ӧ������
�������Բ���������˽�Բ����������2000����ǰ�����ҹ���ī�Ӹ���Բ�ĸ����һ��ͬ��Ҳ��������˼˵��Բ��һ��Բ�ģ�Բ�ĵ�Բ�ܵij�����ȣ���������ϣ����ѧ��ŷ����ø�Բ�µĶ���Ҫ��100�꣮��Բ�йصĶ����кܶ࣬���нǶ�����������֮һ��
���ǰѶ�����Բ�ϣ�һ�ߺ�Բ�ཻ����һ�ߺ�Բ���еĽǽ������нǣ�
���нǶ��������нǵĶ������������л����Ե�Բ�ܽǶ�����
���������нǶ����IJ���֤�����̣�
֤������ͼ�٣�AB���O�����ڵ�A����Բ��O����AC��ʱ�����õ���CAB��90�㣬�������нǡ�BAC�Ķ������������а�Բ���Ե�Բ�ܽǶ�����
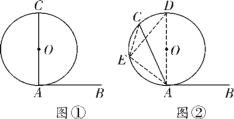
��ͼ�ڣ�AB���O�����ڵ�A����Բ��O�ڡ�BAC���ڲ�ʱ������A��ֱ��AD����O�ڵ�D����![]() ����ȡһ��E������EC��ED��EA�����CED����CAD��
����ȡһ��E������EC��ED��EA�����CED����CAD��
��
����
(1)�밴�������֤��˼·��д����֤����ʣ�ಿ�֣�
(2)��ͼ�ۣ�AB���O�����ڵ�A����Բ��O�ڡ�BAC���ⲿʱ����д�����нǶ�����֤�����̣�
���𰸡���1�������������2���������
��������
��1������Բ�ܽǶ����õ���DEA��90�����ٸ���ͬ�����Ե�Բ�ܽ���ȵõ���CED����CAD��������õ�ʽ�����ʼ��ɵõ���CEA����CAB��
��2��ͨ����C=90��˵����CFA����FAC��90�����ٸ���ͬ�ǵ������ȵõ���CAB����CFA����.
�⣺��1����AD�ǡ�Oֱ����
���DEA��90����
��AB���O�����ڵ�A��
���DAB��90����
���CED����DEA����CAD����DAB������CEA����CAB��
�����нǵĶ������������л����Ե�Բ�ܽǶ�����
��2��֤������ͼ������A��ֱ��AF����O�ڵ�F������FC��
��AF��ֱ����
���ACF��90����
���CFA����FAC��90����
��AB���O�����ڵ�A��
���FAB��90����
���CAB����FAC��90����
���CAB����CFA��
�����нǵĶ������������л����Ե�Բ�ܽǶ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A1B1C1����A2B2C2���ܳ���ȣ����������жϣ�
����A1B1=A2B2��A1C1=A2C2������A1B1C1�ա�A2B2C2��
������A1=��A2����B1=��B2������A1B1C1�ա�A2B2C2��
���������������жϣ�����˵����ȷ���ǣ�������
A. ����ȷ�������� B. ����������ȷ C. �٣��������� D. �٣�������ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
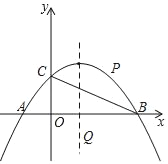
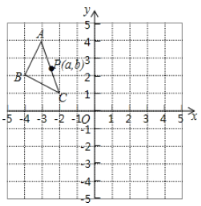
����Ŀ����ͼ����֪��A����1��0����B��3��0����C��0��1����������y=ax2+bx+c�ϣ�
��1���������߽���ʽ��
��2����ֱ��BC�Ϸ�������������һ��P��ʹ��PBC���Ϊ1��
��3����x���·����������߶Գ����ϣ��Ƿ����һ��Q��ʹ��BQC=��BAC�������ڣ����Q�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��4��18�գ�һ��һ�ȵ������ݽ�����������㳡��������ͼ���㳡����һ����A��С��ץ�ŷ����ߵ�һ��վ��D��������ǣ����E��÷���A������Ϊ67����ͬһʱ��Сܿ�ڸ���һ�������30��(BC��30��)�ľ���¥��B����÷���A��������45������֪С�������¥�ľ���CD��40�ף�ǣ���˾����߶�DE��1.5�ף�������������������ݾ����ĸ߶�(�����ȷ��0.1�ף��ο����ݣ�sin67���![]() ��cos67���
��cos67���![]() ��tan67���
��tan67���![]() ��
��![]() ��1.414)��
��1.414)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ѩ��еļṹͼ����ͨ��һ���̶������һ������������������ɼ�ѩ��Ͷѩ�IJ�������������ֱ�ӽӴ�ѩ��ʹ�÷��㣬����С���ѵ�ϲ������ѩ��бպ�ʱ����á�AOB��30�㣬OA��OB��14 cm����˿�ѩ���������ѩ���ֱ��AB�ij���Ϊ________ cm��(�������һλС�����ο����ݣ�sin15���0��26��cos15���0��97��tan15���0��27)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ��������������Ϊ
��������������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��ԭ����ʱ����ת
��ԭ����ʱ����ת![]() ���õ�
���õ�![]() ��
��![]() ����ƽ��6����λ��������ƽ��2����λ�õ�
����ƽ��6����λ��������ƽ��2����λ�õ�![]() ��
��
��1������![]() ��
��![]() ��
��
��2��![]() ��
��![]() ��
��![]() ����һ�㣬
����һ�㣬![]() ����ת��ƽ�ƺ��
����ת��ƽ�ƺ��![]() �Ķ�Ӧ��ֱ�Ϊ
�Ķ�Ӧ��ֱ�Ϊ![]() ��
��![]() �������
�������![]() ��
��![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ɶ����Ǽ����е�һ����Ҫ���������ҹ������顶�����㾭���о����������������ģ����������ļ��أ���ͼ1���ɱ߳���ȵ�С�����κ�ֱ�������ι��ɵģ��������������ϵ��֤���ɶ�����ͼ2����ͼ1��������ڵõ��ģ���֪��BAC=90����AB=6��AC=8����D��E��F��G��H��I���ھ���KLMJ�ı��ϣ������KLMJ���ܳ�Ϊ�� ��

A. 40B. 44C. 84D. 88
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
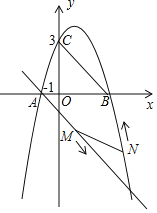
����Ŀ����ͼ�����κ���![]() ��ͼ����x�ύ�ڵ�
��ͼ����x�ύ�ڵ�![]() �͵�B����y�ύ�ڵ�
�͵�B����y�ύ�ڵ�![]() ��
��
![]() ��ö��κ����ı���ʽ��
��ö��κ����ı���ʽ��
![]() ����A��ֱ��
����A��ֱ��![]() �ҽ�����������һ��D����ֱ��AD�ĺ�������ʽ��
�ҽ�����������һ��D����ֱ��AD�ĺ�������ʽ��
![]() ��
��![]() �������£���x�����Ƿ����һ��P��ʹ����B��C��PΪ�������������
�������£���x�����Ƿ����һ��P��ʹ����B��C��PΪ�������������![]() ���ƣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���ƣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У���
�У���![]() Ϊ
Ϊ![]() ��һ�㣬��
��һ�㣬��![]() Ϊ
Ϊ![]() ��һ�㣬��
��һ�㣬��![]() ��
��

(1)��ͼ1����![]() ����֤��
����֤��![]() ��
��
(2)��ͼ2����![]() ����֤��
����֤��![]() ��
��
(3) ��ͼ3����(2)�������£���![]() ����
����![]() ��
��![]() ��ֱ��д���߶�
��ֱ��д���߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com