
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y= ![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).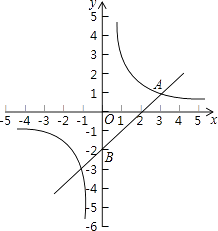
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
【答案】
(1)解:∵反比例函数y= ![]() (m≠0)的图象过点A(3,1),
(m≠0)的图象过点A(3,1),
∴3= ![]()
∴m=3.
∴反比例函数的表达式为y= ![]() .
.
∵一次函数y=kx+b的图象过点A(3,1)和B(0,﹣2).
∴ ![]() ,
,
解得: ![]() ,
,
∴一次函数的表达式为y=x﹣2
(2)解:令y=0,∴x﹣2=0,x=2,
∴一次函数y=x﹣2的图象与x轴的交点C的坐标为(2,0).
∵S△ABP=3,
![]() PC×1+
PC×1+ ![]() PC×2=3.
PC×2=3.
∴PC=2,
∴点P的坐标为(0,0)、(4,0)
【解析】(1)将A点的坐标代入双曲线的解析式即可求出双曲线的解析式,用待定系数法求出一次函数的解析式;
(2)首先求出一次函数y=x﹣2的图象与x轴的交点C的坐标,然后根据三角形的面积求出PC的长度,进而找出P点的坐标。
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某网站策划了A、B两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 30 | 25 | 0.05 |
B | m | n | P |
设每月上网学习时间为x(h)小时,方案A,B的收费金额分别为yA (元)、yB(元).
如图是yB与x之间函数关系的图象
(友情提示:若累计上网时间不超出“包时上网时间”,则只收”月使用费“;若累计上网时间不超出“包时上网时间”,则对超出部分再加收”超时费“)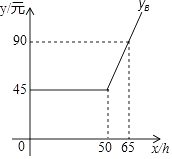
(1)m=;n=p= .
(2)写出yA与x之间的函数关系式.
(3)若每月上网的时间为29小时,请说明选取哪种方式能节省上网费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市上网有两种收费方案,用户可任选其一,A为计时制--1元![]() 时;B为包月制--80元
时;B为包月制--80元![]() 月,此外每种上网方式都附加通讯费
月,此外每种上网方式都附加通讯费![]() 元
元![]() 时.
时.
![]() 某用户每月上网40小时,选哪种方式比较合适?
某用户每月上网40小时,选哪种方式比较合适?
![]() 某用户每月有100元钱用于上网,选哪种方式比较合算?
某用户每月有100元钱用于上网,选哪种方式比较合算?
![]() 请你设计一个方案,使用户能合理地选择上网方式.
请你设计一个方案,使用户能合理地选择上网方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制作一个乙盒需要多用20%的材料。
(1)求制作每个甲盒、乙盒各用多少材料?
(2)如果制作甲、乙两种包装盒3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需材料总长度![]() 与甲盒数量
与甲盒数量![]() 之间的函数关系式,并求出最少需要多少米材料。
之间的函数关系式,并求出最少需要多少米材料。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是( ) 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,线段AE的长为____;
(2)若∠D=35°,∠C=60°,求∠DBC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻落实健康第一的指导思想,促进学生全面发展,国家每年都要对中学生进行一次体能测试,测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级,某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析,并根据收集的数据绘制了两幅不完整的统计图,请根据这两幅统计图中的信息回答下列问题 
(1)本次抽样调查共抽取多少名学生?
(2)补全条形统计图.
(3)在扇形统计图中,求测试结果为“良好”等级所对应圆心角的度数.
(4)若该学校七年级共有600名学生,请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名?
(5)请你对“不及格”等级的同学提一个友善的建议(一句话即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com