
【题目】如图1,已知直线EF//GH,且EF和GH之间的距离为1,小明同学制作了一个直角三角形硬纸板ACB,其中∠ACB=90°,∠BAC=60°,AC=1.小明利用这块三角板进行了如下的操作探究:
(1)如图1,若点C在直线EF上,且∠ACE=20°,求∠1的度数;
(2)若点A在直线EF上,点C在EF和GH之间(不含EF、GH上),边BC、AB与直线GH分别交于点D和点K.
①如图2,∠AKD、∠CDK的平分线交于点O.在△ABC绕着点A旋转的过程中,∠O的度数是否变化?若不变,求出∠O的度数:若变化,请说明理由;
②如图3,在△ABC绕着点A旋转的过程中,设∠EAK=n°,∠CDK=(4m-3n-10)°,求m的取值范围.

【答案】(1)∠1=70°;(2)①∠O的度数不发生变化,∠O=75°;②70°<m<115°.
【解析】
(1)根据两直线平行,内错角相等可得∠1的度数;
(2)①先根据四边形的内角和得∠AKD+∠CDK=360°90°60°=210°,由角平分线的定义和三角形的内角和可得结论;
②先根据①的结论,结合平行线的性质得:n=2m110,确认点C边界上两点时,n的取值,代入n=2m110,可得结论.
解:(1)如图1,∵∠ACB=90°,∠ACE=20°,
∴∠ECB=90°20°=70°,
∵EF∥GH,
∴∠1=∠ECB=70°;
(2)①在△ABC绕着点A旋转的过程中,∠O的度数不发生变化,
理由是:如图2,∵∠BAC=60°,∠ACB=90°,
∴∠AKD+∠CDK=360°90°60°=210°,
∵∠AKD、∠CDK的平分线交于点O,
∴∠OKD=![]() ∠AKD,∠ODK=
∠AKD,∠ODK=![]() ∠CDK,
∠CDK,
∴∠OKD+∠ODK=105°,
∴∠O=180°105°=75°;
②∵EF∥GH,
∴∠EAK=∠AKD=n°,
由①知:∠AKD+∠CDK=210°,
∴n+4m3n10=210,
n=2m110,
如图3,点C在直线EF上时,∠EAK=n=180°60°=120°,

如图4,∵AC=1,且EF和GH之间的距离为1,
∴点C在直线GH上时,∠EAK=n=90°60°=30°,

∵点C在EF和GH之间(不含EF、GH上),
∴30°<n<120°,即30<2m110<120,
∴m的取值范围是:70°<m<115°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) | 120 | 130 | … | 180 |
每天销量y(kg) | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,EF分别交AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD,求证:EG∥FH.

证明:∵AB∥CD( ),
∴∠AEF=∠EFD( ),
∵EG平分∠AEF,FH平分∠EFD( ),
∴∠ =![]() ∠AEF,
∠AEF,
∠ =![]() ∠EFD(角平分线定义),
∠EFD(角平分线定义),
∴∠ =∠ .
∴EG∥FH( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )
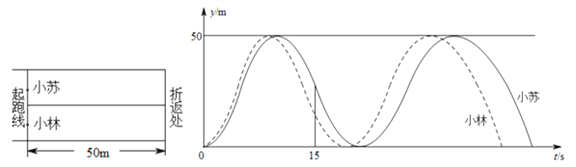
A. 两人从起跑线同时出发,同时到达终点.
B. 小苏跑全程的平均速度大于小林跑全程的平均速度.
C. 小苏在跑最后100m的过程中,与小林相遇2次.
D. 小苏前15s跑过的路程小于小林前15s跑过的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过C,且AD⊥MN于D,BE⊥MN于E.

(1)当直线MN绕点C旋转到图1的位置时,求证:△ADC≌△CEB
(2)当直线MN绕点C旋转到图2的位置时,写出线段DE、AD和BE的数量关系,并说明理由.
(3)当直线MN绕点C旋转到图3的位置时,直接写出DE、AD和BE的数量关系(不用说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据学习函数的经验,对函数y=![]() -5x+4 的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
-5x+4 的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如下表:
x | … |
|
| -2 |
|
| -1 |
|
| 0 |
|
| 1 |
|
| 2 |
| td style="width:17.7pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; border-bottom-style:solid; border-bottom-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">… | |
y | … | 4.3 | 3.2 | 0 | -2.2 | -1.4 | 0 | 2.8 | 3.7 | 4 | 3.7 | 2.8 | 0 | -1.4 | -2.2 | m | 3.2 | 4.3 | … |
其中m= ;
(2)如图,在平面直角坐标系xOy中,描出了以上表中各组对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)观察函数图象,写出一条该函数的性质 ;
(4)进一步探究函数图象发现:
①方程![]() 有 个互不相等的实数根;
有 个互不相等的实数根;
②有两个点(x1,y1)和(x2,y2)在此函数图象上,当x2 >x1>2时,比较y1和y2的大小关系为:
y1 y2 (填“>”、“<”或“=”) ;
③若关于x的方程![]() 有4个互不相等的实数根,则a的取值范围是 .
有4个互不相等的实数根,则a的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
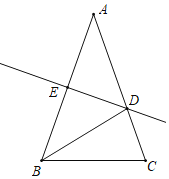
【题目】如图,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠A=40°,求∠DBC的度数.
(2)若△BCD的周长为16cm,△ABC的周长为26cm,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,
沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点.连结MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是【 】

A.一直增大 B.一直减小 C.先减小后增大 D.先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,![]() ,
,![]() 绕点A顺时针旋转,它的两边分别交CB、
绕点A顺时针旋转,它的两边分别交CB、![]() 或它们的延长线
或它们的延长线![]() 于点M、N,当
于点M、N,当![]() 绕点A旋转到
绕点A旋转到![]() 时
时![]() 如图
如图![]() ,则
,则

![]() 线段BM、DN和MN之间的数量关系是______;
线段BM、DN和MN之间的数量关系是______;
![]() 当
当![]() 绕点A旋转到
绕点A旋转到![]() 时
时![]() 如图
如图![]() ,线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
,线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
![]() 当
当![]() 绕点A旋转到
绕点A旋转到![]() 如图
如图![]() 的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com