
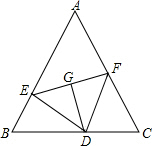
 已知:如图,△ABC中,AB=AC,D是BC上一点,点E、F分别在AB、AC上,BD=CF,CD=BE,G为EF的中点.求证:DG⊥EF.
已知:如图,△ABC中,AB=AC,D是BC上一点,点E、F分别在AB、AC上,BD=CF,CD=BE,G为EF的中点.求证:DG⊥EF.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
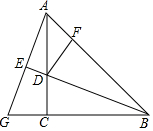 如图:在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F,AE,BC的延长线相交于点G.求证:CD=DF.
如图:在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F,AE,BC的延长线相交于点G.求证:CD=DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为美化校园环境,学校计划在一块肠胃22米,宽为17米的矩形地面上修建同样宽的两条互相垂直的道路(两条道路分别与矩形的一边平行),剩余部分种上花草,并使花草种植面积为300平方米.请问道路宽度为多少米?
如图,为美化校园环境,学校计划在一块肠胃22米,宽为17米的矩形地面上修建同样宽的两条互相垂直的道路(两条道路分别与矩形的一边平行),剩余部分种上花草,并使花草种植面积为300平方米.请问道路宽度为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
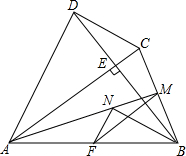 如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.试说明:
如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.试说明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BC是某塔AB在阳光下的影子(将AB,BC看成线段).
如图,BC是某塔AB在阳光下的影子(将AB,BC看成线段).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com