
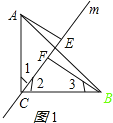
【题目】已知Rt△ABC中,∠C=90°,AC=BC,直线m经过点C,分别过点A,B作直线m的垂线,垂足分别为点E,F,若AE=3,AC=5,则线段EF的长为_______.
【答案】1或7
【解析】分两种情况:①如图1所示:先证出∠1=∠3,由勾股定理求出CE,再证明△BCF≌△CAE,得出对应边相等CF=AE=3,得出EF=CE-CF即可;
②如图2所示:先证出∠1=∠3,由勾股定理求出CE,再证明△BCF≌△CAE,得出对应边相等CF=AE=3,得出EF=CE+CF即可.
分两种情况:①如图1所示:
∵∠ACB=90°,
∴∠1+∠2=90°,
∵BF⊥m,
∴∠BFC=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∵AE⊥m,
∴∠AEC=90°,
∴CE=![]() =4,
=4,
在△BCF和△CAE中,
 ,
,
∴△BCF≌△CAE(AAS),
∴CF=AE=3,
∴EF=CE-CF=4-3=1;
②如图2所示:

∵∠ACB=90°,
∴∠1+∠2=90°,
∵BF⊥m,
∴∠BFC=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∵AE⊥m,
∴∠AEC=90°,
∴CE=![]() =4,
=4,
在△BCF和△CAE中,
 ,
,
∴△BCF≌△CAE(AAS),
∴CF=AE=3,
∴EF=CE+CF=4+3=7;
综上所述:线段EF的长为:1或7.
故答案为:1或7.


科目:初中数学 来源: 题型:
【题目】如图,已知关于x的二次函数y=x2+mx的图象经过原点O,并且与x轴交于点A,对称轴为直线x=1. 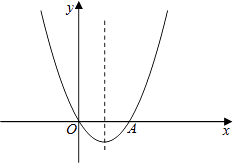
(1)常数m= , 点A的坐标为;
(2)若关于x的一元二次方程x2+mx=n(n为常数)有两个不相等的实数根,求n的取值范围;
(3)若关于x的一元二次方程x2+mx﹣k=0(k为常数)在﹣2<x<3的范围内有解,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
(1)求一次函数y=kx+b的关系式;
(2)结合图象,直接写出满足kx+b>![]()
![]() 的x的取值范围;
的x的取值范围;
(3)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方体的展开图如图所示,如果正方体的六个面分别用字母A,B,C,D,E,F表示,当各面上的数分别与它对面的数互为相反数,且满足B=1,C=﹣a2﹣2a+1,D=﹣1,E=3a+4,F=2﹣a时,求A面表示的数值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
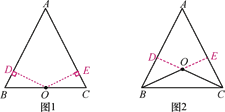
(1)如图1,若点O在BC上,求证:AB=AC.
(2)如图2,若点O在△ABC内部,求证:AB=AC.
(3)猜想,若点O在△ABC的外部,AB=AC成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市为创建“国家园林城市”,某校举行了以“爱我冷江”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图:

根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( ) 
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com