
分析 先将$\left\{{\begin{array}{l}{{x_1}=3}\\{{y_1}=-2}\end{array}}\right.$代入方程组$\left\{{\begin{array}{l}{{x^2}+{y^2}=m}\\{x+y=n}\end{array}}\right.$中求出m、n的值,然后再求方程组的另一组解.
解答 解:将$\left\{{\begin{array}{l}{{x_1}=3}\\{{y_1}=-2}\end{array}}\right.$代入方程组$\left\{{\begin{array}{l}{{x^2}+{y^2}=m}\\{x+y=n}\end{array}}\right.$中得:$\left\{\begin{array}{l}{9+4=m}\\{3-2=n}\end{array}\right.$,
解得:m=13,n=1,
则方程组变形为:$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=13}\\{x+y=1}\end{array}\right.$,
由x+y=1得:x=1-y,
将x=1-y代入方程x2+y2=13中可得:y2-y-6=0,
解得y=3或y=-2,
将y=3代入x+y=1中可得:x=-2,
所以方程的另一组解为:$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=3}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=3}\end{array}\right.$.
点评 本题考查了高次方程,二元一次方程组的解法,熟记解二元一次方程的解法是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | (x2-5)(3x-7)=6x2-29x+35 | B. | (3x+7)(10x-8)=30x2-46x-56 | ||
| C. | (-3x+$\frac{1}{2}$)(-$\frac{1}{3}x$)=x${\;}^{2}-\frac{1}{6}$x | D. | (1-x)(x+1)+(x+2)(x-2)=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
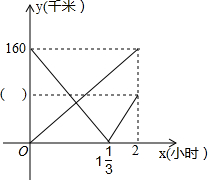 甲乙两地相距240千米,一辆货车从甲地出发驶往乙地,货车行驶一段时间后,一辆轿车从乙地出发驶往甲地,两车与途中一服务区的距离y(千米)与轿车出发时间x(小时)之间的函数关系如图所示:
甲乙两地相距240千米,一辆货车从甲地出发驶往乙地,货车行驶一段时间后,一辆轿车从乙地出发驶往甲地,两车与途中一服务区的距离y(千米)与轿车出发时间x(小时)之间的函数关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
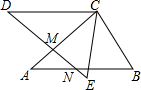 如图,AB=DE,AC=DC,BC=EC,DE与AC、AB分别交于点M、N,CE与AB交于点H,且∠A=∠BCE=40°,∠B=60°
如图,AB=DE,AC=DC,BC=EC,DE与AC、AB分别交于点M、N,CE与AB交于点H,且∠A=∠BCE=40°,∠B=60°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com