
【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.

证明:∵∠AGB=∠EHF(理由: )
∠AGB= (对顶角相等)
∴∠EHF=∠DGF,∴DB∥EC(理由: )
∴ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠D,
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: ).
【答案】已知;∠DGF;同位角相等,两直线平行;∠C; AC;∠A=∠F.
【解析】
分析: 根据对顶角相等推知同位角∠EHF=∠DGF,从而证得两直线DB∥EC;然后由平行线的性质知内错角∠DBA=∠D,即可根据平行线的判定定理推知两直线DF∥AC;最后由平行线的性质(两直线平行,内错角相等)证得∠A=∠F.
详解: ∵∠AGB=∠EHF(已知),∠AGB=∠DGF(对顶角相等),
∴∠EHF=∠DGF
∴DB∥EC(同位角相等,两直线平行),
∴∠C=∠DBA(两直线平行,同位角相等),
又∵∠C=∠D(已知),
∴∠DBA=∠D(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等),
故答案是:已知;∠DGF;同位角相等,两直线平行;C;AC;两直线平行,内错角相等.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y= ![]() x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交y轴于点A3 , …,按此作法进行下去,则OA2017= .
x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交y轴于点A3 , …,按此作法进行下去,则OA2017= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,直线y=mx与双曲线 ![]() 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1. 
(1)求m、n的值;
(2)求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 (小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育老师对自己任教的55名男生进行一百米摸底测试,若规定男生成绩为16秒合格,下表是随机抽取的10名男生分A、B两组测试的成绩与合格标准的差值(比合格标准多的秒数为正,少的秒数为负)。
A 组 | -1.5 | +1.5 | -1 | -2 | -2 |
B组 | +1 | +3 | -3 | +2 | -3 |
(1)请你估算从55名男生中合格的人数大约是多少?
(2)通过相关的计算,说明哪个组的成绩比较均匀;
(3)至少举出三条理由说明A组成绩好于B组成绩,或找出一条理由来说明B组好于A组。
查看答案和解析>>
科目:初中数学 来源: 题型:
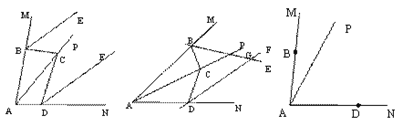
【题目】已知,点B、D分别在∠MAN的两边AM、AN上,点C是射线AP上的一点,连接BC、DC,∠MAN=α,∠BCD=β,(0°<α<180°,0°<β<180°);BE平分∠MBC,DF平分∠NDC.
(1)如图1,若α=β=80°,
①求∠MBC+∠NDC的度数;
②判断BE、DF的位置关系,并说明理由.
(2)如图2,当点C在射线AP上运动时,若直线BE、DF相交于点G,请用含有α、β的代数式表示∠BGD.(直接写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E. 
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点C,若ACAB=12,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ![]() ,反比例函数y=
,反比例函数y= ![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( ) 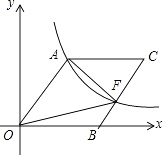
A.60
B.80
C.30
D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的图形,回答下列问题:
(1) 图中的点被线段隔开分成四层,第一层有1个点,第二层有3个点,第三层有5个点,第四层有___________个点;
(2) 如果要你继续画下去,那么第五层有________点, 第10层有_________点;
(3) 某一层上有77个点,你可知道这是第_________层;
(4) 第一层与第二层的和是__________,前三层的和是_________,前四层和为____________,
你有没有发现什么规律?
根据你的推测,前一百层的和是___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com