
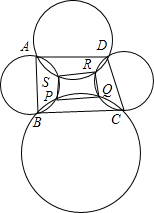
 若以圆内接四边形ABCD的各边为弦作任意圆,求证:这些圆相交的四点共圆.
若以圆内接四边形ABCD的各边为弦作任意圆,求证:这些圆相交的四点共圆. 分析 连接BP、DR,并延长BP、DR,由圆内接四边形的外角等于内对角,得出∠EPS=∠SAB,∠EPQ=∠QCB,∠FRQ=∠QCD,∠FRS=∠SAD,证出∠SPQ+∠SRQ=∠BAD+∠BCD,由圆内接四边形的性质得出∠BAD+∠BCD=180°,得出∠SPQ+∠SRQ=180°,即可得出结论.
解答 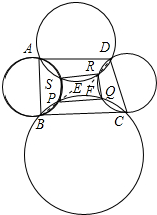 证明:连接BP、DR,并延长BP、DR,如图所示:
证明:连接BP、DR,并延长BP、DR,如图所示:
∵圆内接四边形的外角等于内对角,
∴∠EPS=∠SAB,∠EPQ=∠QCB,∠FRQ=∠QCD,∠FRS=∠SAD,
∴∠EPS+∠EPQ+∠FRQ+∠FRS=∠SAB+∠QCB+∠QCD+∠SAD=∠BAD+∠BCD,
∴∠SPQ+∠SRQ=∠BAD+∠BCD,
∵四边形ABCD是圆内接四边形,
∴∠BAD+∠BCD=180°,
∴∠SPQ+∠SRQ=180°,
∴S、P、Q、R四点共圆.
点评 本题是四点共圆的综合题目,考查了圆内接四边形的性质、四点共圆的判定方法;熟练掌握圆内接四边形的性质,证明四边形PQRS的对角互补是解决问题的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
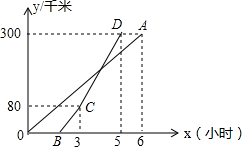 甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地如图、线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系,根据图象解答下列问题:
甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地如图、线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
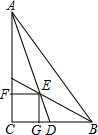 如图,在Rt△ABC中,∠C=90°,∠BAC=40°,AD是△ABC的一条角平分线,点E,F,G分别在AD,AC,BC上,且四边形CGEF是正方形,则∠DEB的度数为( )
如图,在Rt△ABC中,∠C=90°,∠BAC=40°,AD是△ABC的一条角平分线,点E,F,G分别在AD,AC,BC上,且四边形CGEF是正方形,则∠DEB的度数为( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
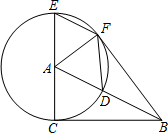 如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.
如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
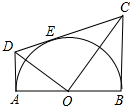 如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )
如图,AB为半圆O的直径,CD切⊙O于点E,AD、BC分别切⊙O于A、B两点,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:①OD2=DE•CD;②AD+BC=CD;③OD=OC;④S梯形ABCD=CD•OA;⑤∠DOC=90°;⑥若切点E在半圆上运动(A、B两点除外),则线段AD与BC的积为定值.其中正确的个数是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
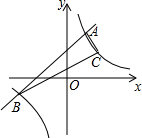 已知一次函数y1=x+5的图象与反比例函数y2=$\frac{k}{x}$的图象交于A、B两点,已知点A的横坐标为1.
已知一次函数y1=x+5的图象与反比例函数y2=$\frac{k}{x}$的图象交于A、B两点,已知点A的横坐标为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
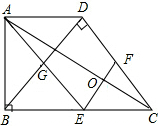 已知:在梯形ABCD中.AD∥BC,∠ABC=90°,∠BDC=90°,BC=2AD,E,F分别是BC、DC的中点.连接AE、EF、AC,连接BD,交AE于点G.
已知:在梯形ABCD中.AD∥BC,∠ABC=90°,∠BDC=90°,BC=2AD,E,F分别是BC、DC的中点.连接AE、EF、AC,连接BD,交AE于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com