
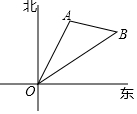
 如图,海岛A在灯塔O处北偏东25°,海岛B在灯塔O处北偏东55°,海岛A在海岛B的北偏西80°,已知海岛A到灯塔的距离为80海里,求海岛B到灯塔的距离.(结果保留根号)
如图,海岛A在灯塔O处北偏东25°,海岛B在灯塔O处北偏东55°,海岛A在海岛B的北偏西80°,已知海岛A到灯塔的距离为80海里,求海岛B到灯塔的距离.(结果保留根号) 分析 根据已知条件得出各角的度数,从而得出∠B的度数,作出AC⊥BO,利用解直角三角形的知识即可求出.
解答 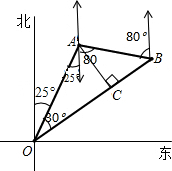 解:过点A作AC⊥OB于C,
解:过点A作AC⊥OB于C,
∵海岛A在灯塔O处北偏东25°,海岛B在灯塔O处北偏东55°,海岛A在海岛B的北偏西80°,
∴∠AOC=30°,∠OAB=25°+80°=105°,
∴∠ABC=45°,
∴AC=BC,
∵海岛A到灯塔的距离为80海里,∠AOC=30°,
∴AC=$\frac{1}{2}$OA=40,即BC=40,
∵cos30°=$\frac{OC}{AO}$,
∴$\frac{\sqrt{3}}{2}$=$\frac{OC}{80}$,
解得:OC=40$\sqrt{3}$,
∴OB=CO+BC=40+40$\sqrt{3}$.
答:海岛B到灯塔的距离是(40+40$\sqrt{3}$)海里.
点评 此题主要考查了方向角问题,作辅助线构造直角三角形是解决问题的关键.在解决有关方向角的问题中,一般要根据题意理清图形中各角的关系,有时所给的方向角并不一定在直角三角形中,需要用到两直线平行内错角相等或一个角的余角等知识转化为所需要的角.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,南湖有一个凉亭A,其正东方向有一棵大树B,一游客想测量A、B之间的距离,他在湖边C处测得A在西南方向,测得B在南偏东33°方向上,且量得B、C之间的距离为50m,求A、B之间的距离(结果精确到0.1m,参考数据:sin33°≈0.545,cos33°≈0.839,tan33°≈0.649)
如图,南湖有一个凉亭A,其正东方向有一棵大树B,一游客想测量A、B之间的距离,他在湖边C处测得A在西南方向,测得B在南偏东33°方向上,且量得B、C之间的距离为50m,求A、B之间的距离(结果精确到0.1m,参考数据:sin33°≈0.545,cos33°≈0.839,tan33°≈0.649)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
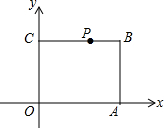 在平面直角坐标系中,点A的坐标为(5,0),点C的坐标为(0,4),四边形ABCO为矩形,点P为线段BC上的一动点,若△POA为等腰三角形,且点P在双曲线y=$\frac{k}{x}$上,则k值可以是10或12或8.
在平面直角坐标系中,点A的坐标为(5,0),点C的坐标为(0,4),四边形ABCO为矩形,点P为线段BC上的一动点,若△POA为等腰三角形,且点P在双曲线y=$\frac{k}{x}$上,则k值可以是10或12或8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:| 成绩x(分) | 频数 | 频率 |
| 50≤x<60 | 10 | a |
| 60≤x<70 | 16 | 0.08 |
| 70≤x<80 | b | 0.20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com