
| A. | a=6,b=4 | B. | a=-6,b=4 | C. | a=6,b=-4 | D. | a=-6,b=-4 |
分析 抛物线的平移,实际上就是顶点的平移,先求出原抛物线的顶点坐标,再根据平移规律,推出新抛物线的顶点坐标,根据顶点式可求新抛物线的解析式.
解答 解:抛物线y=(x-3)2-2的顶点坐标是(3,-2),平移后抛物线y=(x+3)2+2的顶点坐标是(-3,2).
∵点(3,-2)向上平移4个单位,向左平移6个单位得到(-3,2).
∴把函数y=(x-3)2-2的图象向左平移6个单位,再向上平移4(b>0)个单位,所得图象的函数表达式是y=(x+3)2+2,
∴a=6,b=4,
故选:A.
点评 本题考查了抛物线的平移变换.关键是将抛物线的平移转化为顶点的平移,运用顶点式求抛物线解析式.


科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=3,AD=4,顶点A、B、D在坐标轴上.将矩形ABCD平移,使点C与原点O重合,则平移后点A的对应点A′的坐标为(4.8,1.4).
如图,在矩形ABCD中,AB=3,AD=4,顶点A、B、D在坐标轴上.将矩形ABCD平移,使点C与原点O重合,则平移后点A的对应点A′的坐标为(4.8,1.4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
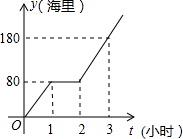 我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.
我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com