
【题目】某商家今年3月份两次同时购进了甲、乙两种不同单价的糖果,第一次购买甲种糖果的数量比乙种糖果的数量多50%,第二次购买甲种糖果的数量比第一次购买甲种糖果的数量少60%,结果第二次购买糖果的总数量虽然比第一次购买糖果的总数量多20%,但第二次购买甲乙糖果的总费用却比第一次购买甲乙糖果的总费用费少10%.(甲,乙两种糖果的单价不变),则乙种糖果的单价是甲种糖果单价的_____%.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m时,水面CD的宽是10m.
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地,已知甲地距此桥280km(桥长忽略不计).货车正以每小时40km的速度开往乙地,当行驶1小时时,忽然接到紧急通知:前方连降暴雨,造成水位以每小时0.25m的速度持续上涨(货车接到通知时水位在CD处,当水位达到桥拱最高点O时,禁止车辆通行),试问:如果货车按原来速度行驶,能否安全通过此桥?若能,请说明理由;若不能,要使货车安全通过此桥,速度应超过每小时多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
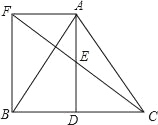
【题目】如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑车从邮局出发,先向西骑行 2 km 到达 A 村,继续向西骑行 3 km 到达 B 村, 然后向东骑行 9 km 到达 C 村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用 1 cm 表示 1 km 画数轴,并在该数轴上表示 A,B,C 三个村庄的位置;
(2)C 村离 A 村有多远?
(3)邮递员一共骑行了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大课间是学校的校体课程之一,涉及的范围广,内容繁多。某校根据实际情况决定开设![]() :乒乓球,
:乒乓球,![]() :篮球,
:篮球,![]() :跑步,
:跑步,![]() :跳绳四种运动项目,为了了解学生最喜欢哪一项运动,随机抽取了600名学生进行调查,并将调查结果绘制成如下的统计图,结合图中信息解答下列问题:
:跳绳四种运动项目,为了了解学生最喜欢哪一项运动,随机抽取了600名学生进行调查,并将调查结果绘制成如下的统计图,结合图中信息解答下列问题:

(1)补全条形统计图;
(2)制作扇形统计图;
(3)若该校有学生2400人,请问:喜欢打乒乓球的学生人数大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”期间,某风景区在![]() 天中每天游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
天中每天游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 |
|
|
|
|
|
|
|
人数变化 单位:万人 |
|
|
|
|
|
| -1.2 |
(1)若![]() 月
月![]() 日的游客人数记为
日的游客人数记为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 月
月![]() 日的游客人数?
日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)此风景区一方面给广大市民提供一个休闲游玩的好去处;另一方面拉动了内需,促进了消费.若![]() 月
月![]() 日的游客人数为
日的游客人数为![]() 万人,进园的人每人平均消费60元,问“十一”期间10月4日游园人员在此风景区的总消费是多少元?(用科学记数法表示)
万人,进园的人每人平均消费60元,问“十一”期间10月4日游园人员在此风景区的总消费是多少元?(用科学记数法表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一副三角板按如图1方式拼接在一起,其中边![]() ,
,![]() 与直线
与直线![]() 重合,
重合,![]() ,
,![]() .
.

(1)图 1 中,![]() =______°.
=______°.
(2)如图2,三角板![]() 固定不动,将三角板
固定不动,将三角板![]() 绕点
绕点![]() 按顺时针方向旋转一个角度
按顺时针方向旋转一个角度![]() ,在转动过程中两块三角板都在直线
,在转动过程中两块三角板都在直线![]() 的上方:
的上方:
①当![]() 平分
平分![]() 、
、![]() 、
、![]() 其中的两边组成的角时,求满足要求的所有旋转角度
其中的两边组成的角时,求满足要求的所有旋转角度![]() 的值;
的值;
②是否存在![]() ?若存在,求此时的
?若存在,求此时的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com