
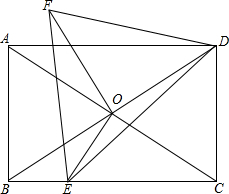
 如图,矩形ABCD的对角线AC、BD交于点O,过点O作OE⊥AC,交BC于点E,将线段OD绕点O逆时针旋转90°得OF,连结FD,FE,DE,已知AB=6,BC=8,则S△EFD=$\frac{149}{8}$.
如图,矩形ABCD的对角线AC、BD交于点O,过点O作OE⊥AC,交BC于点E,将线段OD绕点O逆时针旋转90°得OF,连结FD,FE,DE,已知AB=6,BC=8,则S△EFD=$\frac{149}{8}$. 分析 如图,作EM⊥BD于M,EN⊥EO于N.由△COE∽△CBA,得$\frac{CE}{AC}$=$\frac{CO}{CB}$,求出CE、BE,由△BME∽△BCD,得$\frac{BM}{BC}$=$\frac{BE}{BD}$=$\frac{EM}{CD}$,求出EM、EN,根据S△EFD=S△EOF+S△EOD+S△FOD即可解决问题.
解答 解:如图,作EM⊥BD于M,EN⊥EO于N.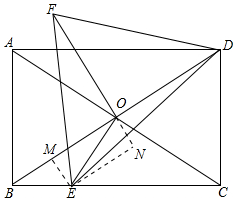
∵四边形ABCD是矩形,
∴AB=CD=6,BC=AD=8,OA=OC=OB=OD,∠ABC=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵OE⊥AC,
∴∠EOC=∠ABC=90°,∵∠ECO=∠ACB,
∴△COE∽△CBA,
∴$\frac{CE}{AC}$=$\frac{CO}{CB}$,
∴$\frac{CE}{10}$=$\frac{5}{8}$,
∴CE=$\frac{25}{4}$,BE=BC-CE=$\frac{7}{4}$,
∵∠EBM=∠CBD,∠EMB=∠BCD=90°,
∴△BME∽△BCD,
∴$\frac{BM}{BC}$=$\frac{BE}{BD}$=$\frac{EM}{CD}$,
∴EM=$\frac{21}{20}$,BM=$\frac{7}{5}$,
∴S△EFD=S△EOF+S△EOD+S△FOD=$\frac{1}{2}$×5×$\frac{21}{20}$+$\frac{1}{2}$×5×$\frac{7}{5}$+$\frac{1}{2}$×5×5=$\frac{149}{8}$.
故答案为$\frac{149}{8}$.
点评 本题考查矩形的性质.旋转变换三角形的面积等知识,解题的关键是学会添加常用辅助线,学会利用分割法求三角形面积,属于中考常考题型.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
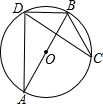 如图,D、C是⊙O上的两点,AB经过圆心O,若∠C=30°,AD=3,则⊙O的直径为( )
如图,D、C是⊙O上的两点,AB经过圆心O,若∠C=30°,AD=3,则⊙O的直径为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
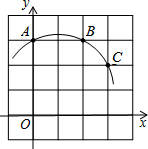 如图,在带有正方形网格的平面直角坐标系xOy中,一条圆弧经过A(0,3),B(2,3),C(3,2)三点,那么这条圆弧所在圆的圆心坐标是( )
如图,在带有正方形网格的平面直角坐标系xOy中,一条圆弧经过A(0,3),B(2,3),C(3,2)三点,那么这条圆弧所在圆的圆心坐标是( )| A. | (0,0) | B. | (1,1) | C. | (0,1) | D. | (1,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com