
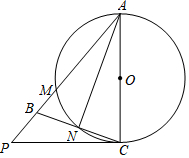
 如图,在△ABC中,AB=AC,以AC为直径的⊙O交与点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交与点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.分析 (1)由AC为⊙O直径,得到∠NAC+∠ACN=90°,由AB=AC,得到∠BAN=∠CAN,根据PC是⊙O的切线,得到∠ACN+∠PCB=90°,于是得到结论.
(2)由等腰三角形的性质得到∠ABC=∠ACB,根据圆内接四边形的性质得到∠PBC=∠AMN,证出△BPC∽△MNA,即可得到结论.
解答 (1)证明:∵AC为⊙O直径,
∴∠ANC=90°,
∴∠NAC+∠ACN=90°,
∵AB=AC,
∴∠BAN=∠CAN,
∵PC是⊙O的切线,
∴∠ACP=90°,
∴∠ACN+∠PCB=90°,
∴∠BCP=∠CAN,
∴∠BCP=∠BAN;
(2)∵AC=4,PC=3,
∴AP=5,
∴PB=1,
∵PC是⊙O的切线,
∴PC2=PM•PA,
∴PM=$\frac{9}{5}$,
∴AM=$\frac{16}{5}$,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠PBC+∠ABC=∠AMN+∠ACN=180°,
∴∠PBC=∠AMN,
由(1)知∠BCP=∠BAN,
∴△BPC∽△MNA,
∴$\frac{PB}{MN}$=$\frac{BC}{AM}$,
∴MN•BC=PB•AM=$\frac{16}{5}$.
点评 本题考查了切线的性质,等腰三角形的性质,圆周角定理,相似三角形的判定和性质,圆内接四边形的性质,解此题的关键是熟练掌握定理.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
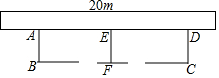 如图,星光中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙(墙的长度为20m),其余部分用篱笆围成,且中间用一段篱笆把它分隔成了两个矩形,两个矩形各留一道1m宽的门,已知篱笆的总长度为34m.
如图,星光中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙(墙的长度为20m),其余部分用篱笆围成,且中间用一段篱笆把它分隔成了两个矩形,两个矩形各留一道1m宽的门,已知篱笆的总长度为34m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在全国初中数学联赛中,将参赛两个班学生的成绩(得分均为整数)进行整理后分成五组,绘制出如下的频率分布直方图(如图所示),已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.25、0.15、0.10、0.10,第二组的频数是40.
在全国初中数学联赛中,将参赛两个班学生的成绩(得分均为整数)进行整理后分成五组,绘制出如下的频率分布直方图(如图所示),已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.25、0.15、0.10、0.10,第二组的频数是40.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
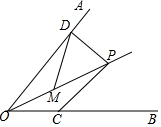 如图,已知点P是∠AOB平分线上一点,∠AOB=60°,PD⊥OA,垂足为D,M是OP上一点,连接MD,MD=MP,OM=4cm,点C是OB上一个动点,则PC的最小值为( )
如图,已知点P是∠AOB平分线上一点,∠AOB=60°,PD⊥OA,垂足为D,M是OP上一点,连接MD,MD=MP,OM=4cm,点C是OB上一个动点,则PC的最小值为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 1cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com