
| A型 | B型 | |
| 价格(万元/台) | 12 | 10 |
| 处理污水量(吨/月) | 240 | 200 |
分析 (1)关键描述语:企业购买设备的资金不高于105万元,列出不等式进行求解.
(2)关键描述语:每月A和B型两种设备的污水处理量应大于等于2040吨,且为了节约资金,所需的费用应为最少.
解答 解:(1)设买x台A型,则买 (10-x)台B型,根据题意得:
12x+10(10-x)≤105,
解得:x≤$\frac{5}{2}$.
答:可买10台B型;或 1台A型,9台B型;或2台A型,8台B型;
(2)设买x台A型,则由题意可得
240x+200(10-x)≥2040,
解得 x≥1.
当x=1时,花费 12×1+10×9=102 (万元);
当x=2时,花费 12×2+10×8=104 (万元)
答:买1台A型,9台B型设备时最省钱.
点评 本题主要考查一元一次不等式的应用,通过运用数学模型,可使求解过程变得简单.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
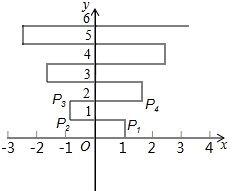 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第99次跳动至点P99的坐标是( )
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第99次跳动至点P99的坐标是( )| A. | (26,50) | B. | (-26,50) | C. | (25,50) | D. | (-25,50) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC.
如图,△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D是BC边上一点,直线ED⊥BC于点D,交AB于点E,CF∥AB交直线DE于点F,设CD=x
如图,在△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D是BC边上一点,直线ED⊥BC于点D,交AB于点E,CF∥AB交直线DE于点F,设CD=x查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com