
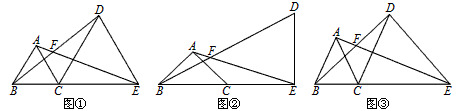
| 解:⑴∠AFB=60°,∠AFB=45°; ⑵∠AFB=90°-  α α⑶图4中:∠AFB=90°-  α; α;图5中:∠AFB=90°+  α。 α。∠AFB=90°-  α的证明如下: α的证明如下:∵AB=AC,EC=ED,∠BAC=∠CED, ∴△ABC∽△EDC, ∴∠ACB=∠ECD,  , ,∴∠BCD=∠ACE, ∴△BCD∽△ACE, ∴∠CBD=∠CAE, ∴∠AFB=180°-∠CAE-∠BAC-∠ABD=180°-∠BAC-∠ABC=∠ACB, ∵AB=AC,∠BAC=α, ∴∠ACB=90-  α, α,∴∠AFB=90°-  α; α;∠AFB=90°+  α的证明如下: α的证明如下:∵AB=AC,EC=ED,∠BAC=∠CED, ∴△ABC∽△EDC, ∴∠ACB=∠ECD,  , ,∴∠BCD=∠ACE, ∴△BCD∽△ACE, ∴∠BDC=∠AEC, ∴∠AFB=∠BDC+∠CDE+∠DEF=∠CDE+∠CED=180°-∠DCE, ∵AB=AC,EC=ED,∠BAC=∠DCE=α, ∴∠DCE=90-  α, α,∴∠AFB=180°-(90-  α)=90°+ α)=90°+ α。 α。 |
  |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:2010-2011学年广东省考数学模拟试卷(三) 题型:解答题
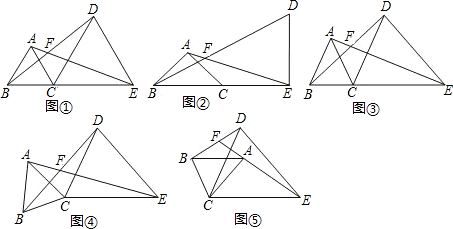
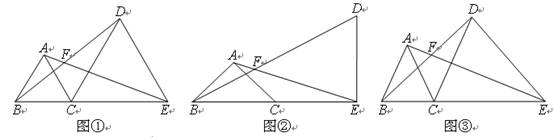
(本题满分9分)填空或解答:点B、C、E在同一直线上,点A、D在直线CE
的同侧,AB=AC,EC=ED,∠BAC=∠CED,直线AE、BD交于点F。
(1)如图①,若∠BAC=60°,则∠AFB=_________;如图②,若∠BAC=90°,则∠AFB=_________;
(2)如图③,若∠BAC=α,则∠AFB=_________(用含α的式子表示);
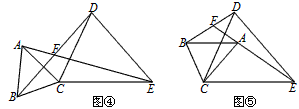
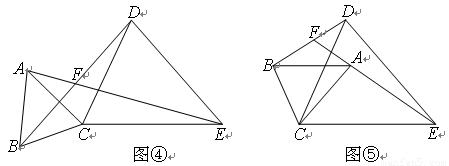
(3)将图③中的△ABC绕点C旋转(点F不与点A、B重合),得图④或图⑤。
在图④中,∠AFB与∠α的数量关系是________________;
在图⑤中,∠AFB与∠α的数量关系是________________。请你任选其中一个结论证明。
查看答案和解析>>
科目:初中数学 来源:第25章《图形的变换》中考题集(17):25.2 旋转变换(解析版) 题型:解答题
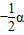 ;在图⑤中,∠AFB与∠α的数量关系是______.请你任选其中一个结论证明.
;在图⑤中,∠AFB与∠α的数量关系是______.请你任选其中一个结论证明.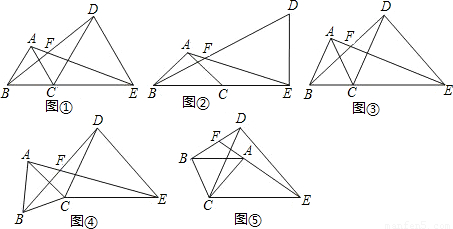
查看答案和解析>>
科目:初中数学 来源:2009-2010学年福建省宁德市福鼎一中九年级(上)期末数学试卷(解析版) 题型:解答题
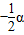 ;在图⑤中,∠AFB与∠α的数量关系是______.请你任选其中一个结论证明.
;在图⑤中,∠AFB与∠α的数量关系是______.请你任选其中一个结论证明.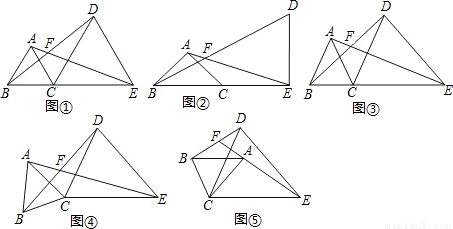
查看答案和解析>>
科目:初中数学 来源:第24章《图形的相似》中考题集(17):24.3 相似三角形(解析版) 题型:解答题
 ;在图⑤中,∠AFB与∠α的数量关系是______.请你任选其中一个结论证明.
;在图⑤中,∠AFB与∠α的数量关系是______.请你任选其中一个结论证明.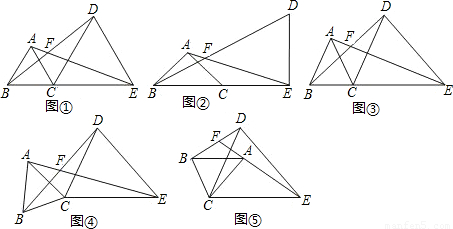
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com