
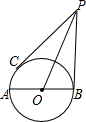
 如图,已知点C在以AB为直径的⊙O上,过点B、C作⊙O的切线,且交于点P,联结AC,若OP=$\frac{9}{2}$AC.求$\frac{PB}{AC}$的值.
如图,已知点C在以AB为直径的⊙O上,过点B、C作⊙O的切线,且交于点P,联结AC,若OP=$\frac{9}{2}$AC.求$\frac{PB}{AC}$的值. 分析 连接OC、BC,根据切线的性质得到∠POC=∠POB.由圆周角定理得到∠COB=2∠OAC,等量代换得到∠POB=∠OAC,根据平行线的判定得到OP∥AC,推出△BAC∽△POB,由相似三角形的性质得到$\frac{AC}{OB}=\frac{AB}{OP}$,设r为⊙O的半径,于是得到AB=2r,OB=r,代入比例式得到OP=3r,AC=$\frac{2}{3}$r,由勾股定理得PB=$\sqrt{O{P}^{2}-O{B}^{2}}$=2$\sqrt{2}$r,即可得到结论.
解答 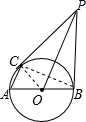 解:连接OC、BC,
解:连接OC、BC,
∵PC、PB为⊙O的切线,
∴∠POC=∠POB.
又∵∠COB=2∠OAC,
∴∠POB=∠OAC,
∴OP∥AC,
∵AB是⊙O的直径,
∴∠ACB=∠OBP=90°,
∴△BAC∽△POB,
∴$\frac{AC}{OB}=\frac{AB}{OP}$,
设r为⊙O的半径,
∴AB=2r,OB=r,
∵OP=$\frac{9}{2}$AC,
∴OP=3r,AC=$\frac{2}{3}$r,
在Rt△POB 中,由勾股定理得PB=$\sqrt{O{P}^{2}-O{B}^{2}}$=2$\sqrt{2}$r,
∴$\frac{PB}{AC}$=$\frac{2\sqrt{2}r}{\frac{2}{3}r}$=3$\sqrt{2}$.
点评 本题考查了切线的性质,相似三角形的判定和性质,勾股定理,圆周角定理,熟练掌握切线的性质是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | w=-200x2+3700x-80000 | B. | w=-200x2+3200x | ||
| C. | w=-200x2-800 | D. | 以上答案都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 投中次数 | 0 | 1 | 2 | 3 | 4 |
| 学生人数 | 3 | 5 | 6 | x | 2 |
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向右平移4个单位长度得到 | B. | 向左平移2个单位长度得到 | ||
| C. | 向上平移2个单位长度得到 | D. | 向下平移4个单位长度得到 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
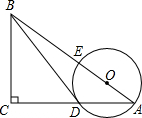 在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA的长为半径的圆分别交AC,AB于点D、E,且BD为⊙O的切线,
在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA的长为半径的圆分别交AC,AB于点D、E,且BD为⊙O的切线,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
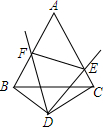 已知△ABC是边长为2的等边三角形,△DBC是顶角为120°的等腰三角形,以点D为顶点作一个60°角,角的两边分别交AB,AC于点E,F,连接EF,则△AEF的周长=4.
已知△ABC是边长为2的等边三角形,△DBC是顶角为120°的等腰三角形,以点D为顶点作一个60°角,角的两边分别交AB,AC于点E,F,连接EF,则△AEF的周长=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2?(-2)=-2 | B. | a?b=b?a | ||
| C. | 若a+b=0,则(a?a)+(b?b)=2ab | D. | 若a?b=0,则a=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个零件的形状如图所示,按规定∠A应等于120°,∠B、∠D应分别为15°、20°.李叔叔量得∠BCD=145°,就能断定该零件不合格,你能说出其中的道理吗?
一个零件的形状如图所示,按规定∠A应等于120°,∠B、∠D应分别为15°、20°.李叔叔量得∠BCD=145°,就能断定该零件不合格,你能说出其中的道理吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com