练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    等式的性质1：等式的两边都加上(或都减去)同一个数或式，所得结果仍是________；

    等式的性质2：等式的两边同乘以(或都除以)同一个不为零的数或式，所得结果仍是________．

    答案：等式;等式
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    10、情景再现：
    利用等式的性质解下列方程
    （1）x+1=6（2）3-x=7
    解：（1）方程两边都同时减去1，得：
    x+1-1=6-1  x=6-1  x=5
    （2）方程两边都加上x得
    3-x+x=7+x  3=7+x
    方程两边都减去7得
    3-7=7+x-7
    ∴-4=x
    习惯上写成：x=-4
    观察上面解的过程实际是把原方程中已知项“+1”，改变符号后从方程左边移到了右边．这种变形叫做移项．
    观察并思考第（2）小题中有哪一项被移项了：
    x、7
    ．
    利用移项解下列方程
    （1）x-5=11        （2）3=11-x
    解：移项得
    x=11+5
    解：移项得
    x=11-3

    ∴x=
    x=16
    ∴
    x=8

    ∴x=
    16

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    20、如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足为D，∠BCD=35°，
    求：（1）∠EBC的度数；（2）∠A的度数．
    对于上述问题，在以下解答过程的空白处填上适当的内容（理由或数学式）．
    解：（1）∵CD⊥AB（已知）
    ∴∠CDB=
    90°

    ∵∠EBC=∠CDB+∠BCD
    三角形的外角等于与它不相邻两个内角的和

    ∴∠EBC=
    90°
    +35°=
    125°
    ．（等量代换）
    （2）∵∠EBC=∠A+ACB
    三角形的外角等于与它不相邻两个内角的和

    ∴∠A=∠EBC-∠ACB．（等式的性质）
    ∵∠ACB=90°（已知）
    ∴∠A=
    125°
    -90°=
    35°
    ．（等量代换）

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

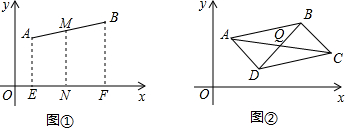    让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系．
    第一步：数轴上两点连线的中点表示的数．自己画一个数轴，如果点A、B分别表示-2、4，则线段AB的中点M表示的数是
    1
    1
    ． 再试几个，我们发现：数轴上连接两点的线段的中点所表示的数是这两点所表示数的平均数．
    第二步；平面直角坐标系中两点连线的中点的坐标（如图①）为便于探索，我们在第一象限内取两点A（x1，y1），B（x2，y2），取线段AB的中点M，分别作A、B到x轴的垂线段AE、BF，取EF的中点N，则MN是梯形AEFB的中位线，故MN⊥x轴，利用第一步的结论及梯形中位线的性质，我们可以得到点M的坐标是（
    x1+x2
    2
    x1+x2
    2
    ，
    y1+y2
    2
    y1+y2
    2
     ）（用x1，y1，x2，y2表示），AEFB是矩形时也可以．我们的结论是：平面直角坐标系中连接两点的线段的中点的横（纵）坐标等于这两点的横（纵）坐标的平均数．
    第三步：平面直角坐标系中平行四边形的顶点坐标之间的关系（如图②）在平面直角坐标系中画一个平行四边形ABCD，设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），则其对角线交点Q的坐标可以表示为Q（
    x1+x3
    2
    x1+x3
    2
    ，
    y1+y3
    2
    y1+y3
    2
    ），也可以表示为Q（
    x2+x4
    2
    x2+x4
    2
    ，
    y2+y4
    2
    y2+y4
    2
     ），经过比较，我们可以分别得出关于x1，x2，x3，x4及，y1，y2，y3，y4的两个等式是
    x1+x3=x2+x4
    x1+x3=x2+x4
    和
    y1+y3=y2+y4
    y1+y3=y2+y4
    ． 我们的结论是：平面直角坐标系中平行四边形的对角顶点的横（纵）坐标的
    和相等
    和相等
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读小明解方程的过程回答问题．
    解方程：2x+9=3（x+2）
    步骤①2x+9=3x+6
    步骤②2x-6=3x-9
    步骤③2（x-3）=3（x-3）
    步骤④2-3
    （1）上述变形中，由步骤①到步骤②变形的依据是
    等式的基本性质或移项法则
    等式的基本性质或移项法则
    ．
    （2）你认为上述变形正确吗，如果不正确请指出错误的步骤，并说明不正确的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系。
    第一步：数轴上两点连线的中点表示的数
    自己画一个数轴，如果点A、B分别表示-2、4，则线段AB的中点M表示的数是                。 再试几个，我们发现：
    数轴上连结两点的线段的中点所表示的数是这两点所表示数的平均数。
    第二步；平面直角坐标系中两点连线的中点的坐标（如图①）
    为便于探索，我们在第一象限内取两点A（x1,y1），B（x2,y2）,取线段AB的中点M，分别作A、B到x轴的垂线段AE、BF，取EF的中点N，则MN是梯形AEFB的中位线，故MN⊥x轴，利用第一步的结论及梯形中位线的性质，我们可以得到点M的坐标是（             ，                     ）（用x1,y1，x2,y2表示），AEFB是矩形时也可以。我们的结论是：平面直角坐标系中连结两点的线段的中点的横（纵）坐标等于这两点的横（纵）坐标的平均数。
        
    图①                    图②
    第三步：平面直角坐标系中平行四边形的顶点坐标之间的关系（如图②）
    在平面直角坐标系中画一个平行四边形ABCD，设A（x1,y1），B（x2,y2），C（x3,y3）,
    D（x4,y4）,则其对角线交点Q的坐标可以表示为Q（            ，         ），也可以表示为Q（             ，          ），经过比较，我们可以分别得出关于x1,x2,x3,x4及,y1,y2,y3,y4的两个等式是            和                          。 我们的结论是：平面直角坐标系中平行四边形的对角顶点的横（纵）坐标的              。

    查看答案和解析>>

    同步练习册答案