
【题目】直线![]() 与直线
与直线![]() 垂直相交于点
垂直相交于点![]() ,点
,点![]() 在射线
在射线![]() 上运动(点
上运动(点![]() 不与点
不与点![]() 重合),点
重合),点![]() 在射线
在射线![]() 上运动(点
上运动(点![]() 不与点
不与点![]() 重合).
重合).
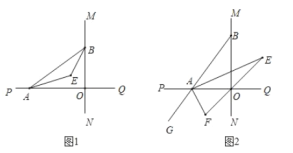
(1)如图1,已知![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的角平分线,
的角平分线,
①当![]() 时,求
时,求![]() 的度数;
的度数;
②点![]() 在运动的过程中,
在运动的过程中,![]() 的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出
的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出![]() 的大小;
的大小;
(2)如图2,延长![]() 至
至![]() ,已知
,已知![]() 、
、![]() 的角平分线与
的角平分线与![]() 的角平分线所在的直线分别相交于
的角平分线所在的直线分别相交于![]() 、
、![]() ,在
,在![]() 中,如果有一个角是另一个角的3倍,请直接写出
中,如果有一个角是另一个角的3倍,请直接写出![]() 的度数.
的度数.
【答案】(1)∠AEB的大小不会发生变化,∠AEB的度数是135°;(2)60°或45°.理由见解析.
【解析】
(1)①根据三角形内角和定理、角分线定义即可求得∠AEB的度数;
②与①同理,只是把具体度数转化为角表示出来即可得结论;
(2)根据三角形内角和定理及一个外角等于与它不相邻的两个内角和,分四种情况讨论即可.
(1)如图1,①∵MN⊥PQ,∴∠AOB=90°.
∵∠ABO=60°,∴∠BAO=30°.
∵AE、BE分别是∠BAO和∠ABO的角平分线,∴∠ABE![]() ∠ABO=30°,∠BAE
∠ABO=30°,∠BAE![]() ∠BAO=15°,∴∠AEB=180°﹣∠ABE﹣∠BAE=180°﹣30°-15°=135°.
∠BAO=15°,∴∠AEB=180°﹣∠ABE﹣∠BAE=180°﹣30°-15°=135°.
答:∠AEB的度数是135°.
②∠AEB的大小不会发生变化.理由如下:
同①,得:∠AEB=180°﹣∠ABE﹣∠BAE=180°![]() ∠ABO
∠ABO![]() ∠BAO=180°
∠BAO=180°![]() (∠ABO+∠BAO)=180°
(∠ABO+∠BAO)=180°![]() 90°=135°.
90°=135°.
答:∠AEB的大小不会发生变化,∠AEB的度数是135°.
(2)∠ABO的度数为60°或45°.理由如下:
如图2.
∵∠BAO、∠OAG的角平分线与∠BOQ的角平分线所在的直线分别相交于E、F,∴∠OAE+∠OAF![]() (∠BAO+∠GAO)=90°,即∠EAF=90°.
(∠BAO+∠GAO)=90°,即∠EAF=90°.
∵AE、OE是角平分线,∴∠BAE=∠EAO,∠BOE=∠EOQ,∴∠ABO +∠BAO=∠BOQ=90°=2∠EOQ=2(∠E+∠EAO),∴∠ABO +2∠EAO=2∠E+2∠EAO,∴∠E=![]() ∠ABO.
∠ABO.
∵∠FAE=90°,∴∠F+∠E=90°,∴∠F=90°-∠E=90°-![]() ∠ABO.
∠ABO.
分四种情况讨论:
①当∠FAE=3∠E时,∠E=90°÷3=30°,∠ABO =2∠E=60°;
②当∠FAE=3∠F时,∠F=90°÷3=30°,∴90°-![]() ∠ABO =30°,解得:∠ABO =120°>90°,故舍去;
∠ABO =30°,解得:∠ABO =120°>90°,故舍去;
③当∠F=3∠E时,90°-![]() ∠ABO =3×
∠ABO =3×![]() ∠ABO,解得:∠ABO =45°;
∠ABO,解得:∠ABO =45°;
④当3∠F=∠E时,3×(90°-![]() ∠ABO)=
∠ABO)=![]() ∠ABO,解得:∠ABO =135°>90°,故舍去.
∠ABO,解得:∠ABO =135°>90°,故舍去.
综上所述:∠ABO的度数是60°或45°.
故答案为:60°或45°.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】小明同学将某班级毕业升学体育测试成绩(满分30分)统计整理,得到下表,则下列说法错误的是( )
分数 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
人数 | 2 | 4 | 3 | 8 | 10 | 9 | 6 | 3 | 1 |
A. 该组数据的众数是24分
B. 该组数据的平均数是25分
C. 该组数据的中位数是24分
D. 该组数据的极差是8分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7 月 9 日,滴滴发布北京市滴滴网约车价格调整,公布了新的滴滴快车计价规则,车费由“总里程费+总时长费”两部分构成,不同时段收费标准不同,具体收费标准如下表,如果车费不足起步价,则按起步价收费.
时间段 | 里程费(元/千米) | 时长费(元/分钟) | 起步价(元) |
06:00-10:00 | 1.80 | 0.80 | 14.00 |
10:00-17:00 | 1.45 | 0.40 | 13.00 |
17:00-21:00 | 1.50 | 0.80 | 14.00 |
21:00-6:00 | 2.15 | 0.80 | 14.00 |
(1)小明早上 7:10 乘坐滴滴快车上学,行车里程 6 千米,行车时间 10 分钟,则应付车费多少元?
(2)小云 17:10 放学回家,行车里程 1 千米,行车时间 15 分钟,则应付车费多少元?
(3)下晚自习后小明乘坐滴滴快车回家,20:45 在学校上车,由于堵车,平均速度是 a 千米/小时,15 分钟后走另外一条路回家,平均速度是 b 千米/小时,5 分钟后到家,则他应付车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
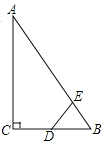
【题目】如图,Rt△ABC中,![]() ,
,![]() ,
,![]() ,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿AB向B点运动,设E点的运动时间为t秒,连接DE,当以B、D、E为顶点的三角形与△ABC相似时,t的值为( )
,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿AB向B点运动,设E点的运动时间为t秒,连接DE,当以B、D、E为顶点的三角形与△ABC相似时,t的值为( )
A.2或3.5B.2或3.2C.2或3.4D.3.2或3.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送5批客人,行驶路程记录如下(规定向东为正,向西为负,单位:km):
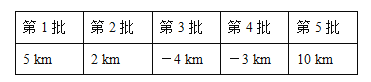
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为引导学生广泛阅读文学名著,某校在七年级、八年级开展了读书知识竞赛.该校七、八年级各有学生400人,各随机抽取20名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
七年级:
74 97 96 89 98 74 65 76 72 78 99 72 97 76 99 74 99 73 98 74
八年级:
76 88 93 65 78 94 89 68 95 50 89 88 89 89 77 94 87 88 92 91
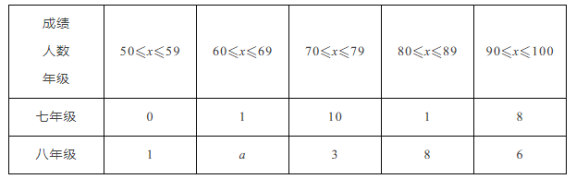
平均数、中位数、众数如表所示:
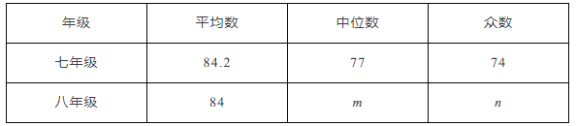
根据以上信息,回答下列问题:
(1)![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)该校对读书知识竞赛成绩不少于80分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有______人;
(3)结合以上数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平行四边形ABCD在平面直角坐标系中,A、B(点A在点B的左侧)两点的横坐标是方程![]() 的两个根,点D在y轴上其中
的两个根,点D在y轴上其中![]() .
.

(1)求平行四边形ABCD的面积;
(2)若P是第一象限位于直线BD上方的一点,过P作![]() 于E,过E作
于E,过E作![]() 轴于H点,作PF∥y轴交直线BD于F,F为BD中点,其中△PEF的周长是
轴于H点,作PF∥y轴交直线BD于F,F为BD中点,其中△PEF的周长是![]() ;若M为线段AD上一动点,N为直线BD上一动点,连接HN,NM,求
;若M为线段AD上一动点,N为直线BD上一动点,连接HN,NM,求![]() 的最小值,此时y轴上有一个动点G,当
的最小值,此时y轴上有一个动点G,当![]() 最大时,求G点坐标;
最大时,求G点坐标;
(3)在(2)的情况下,将△AOD绕O点逆时针旋转60°后得到![]() 如图2,将线段
如图2,将线段![]() 沿着x轴平移,记平移过程中的线段
沿着x轴平移,记平移过程中的线段![]() 为
为![]() ,在平面直角坐标系中是否存在点S,使得以点
,在平面直角坐标系中是否存在点S,使得以点![]() ,
,![]() ,E,S为顶点的四边形为菱形,若存在,请求出点S的坐标,若不存在,请说明理由.
,E,S为顶点的四边形为菱形,若存在,请求出点S的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次为地震灾区的捐款活动中,某校随机调查了50名学生的捐款情况,统计如表:
捐款金额(元) | 5 | 10 | 15 | 20 | 50 |
捐款人数(人) | 7 | 18 | 10 | 12 | 3 |
(1)这50名学生捐款金额的众数和中位数分别为多少元?
(2)如果把这50名学生的捐款情况绘制成扇形统计图,则捐款金额为15元的人数所对应的扇形圆心角为多少度?
(3)若该校共有1200名学生,估计该校的捐款总数大约是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com